Предмет: Алгебра,
автор: zeroo0591
Решите неравенство, с условиями, если они требуются.
Приложения:
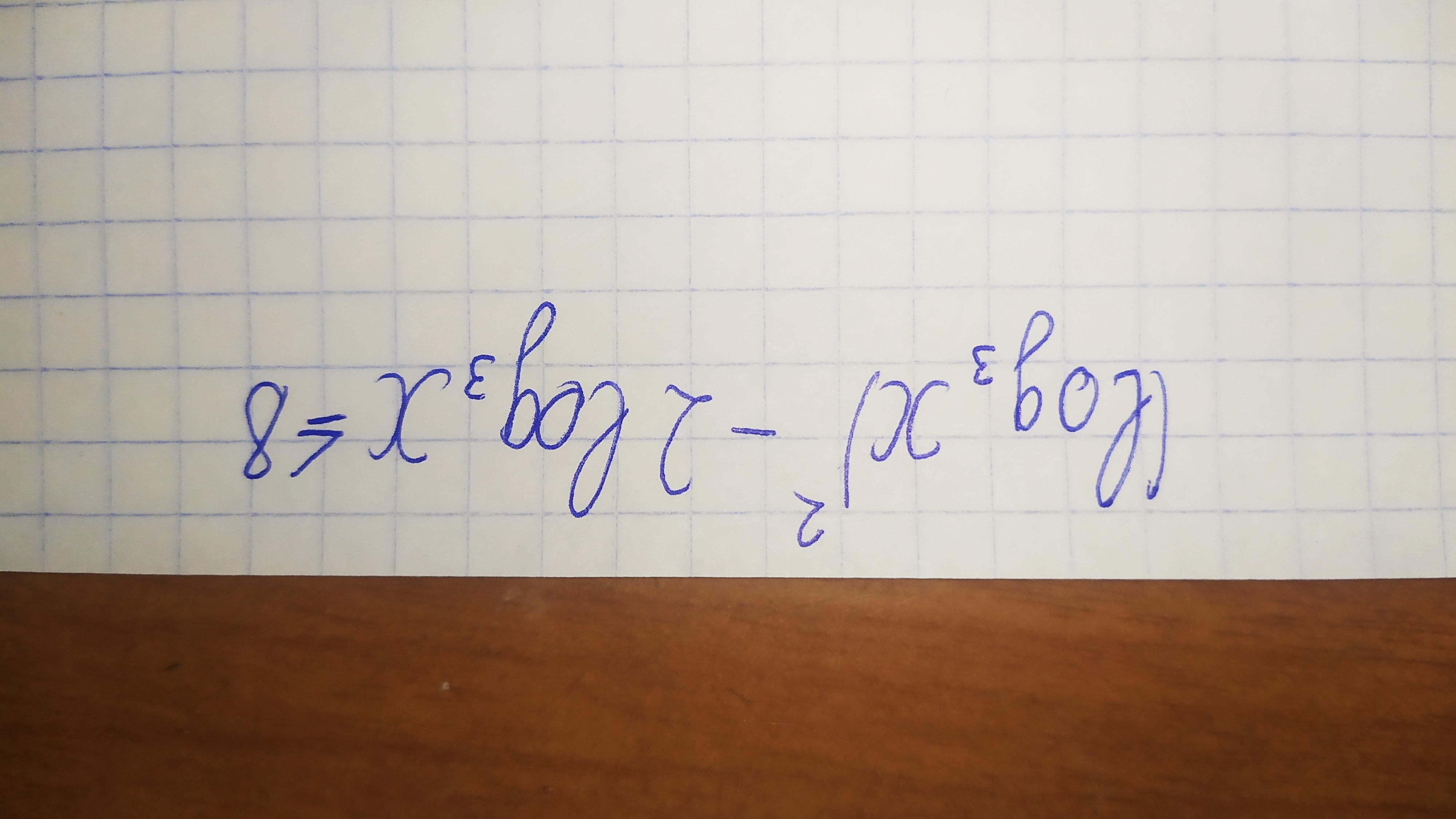
Ответы
Автор ответа:
1
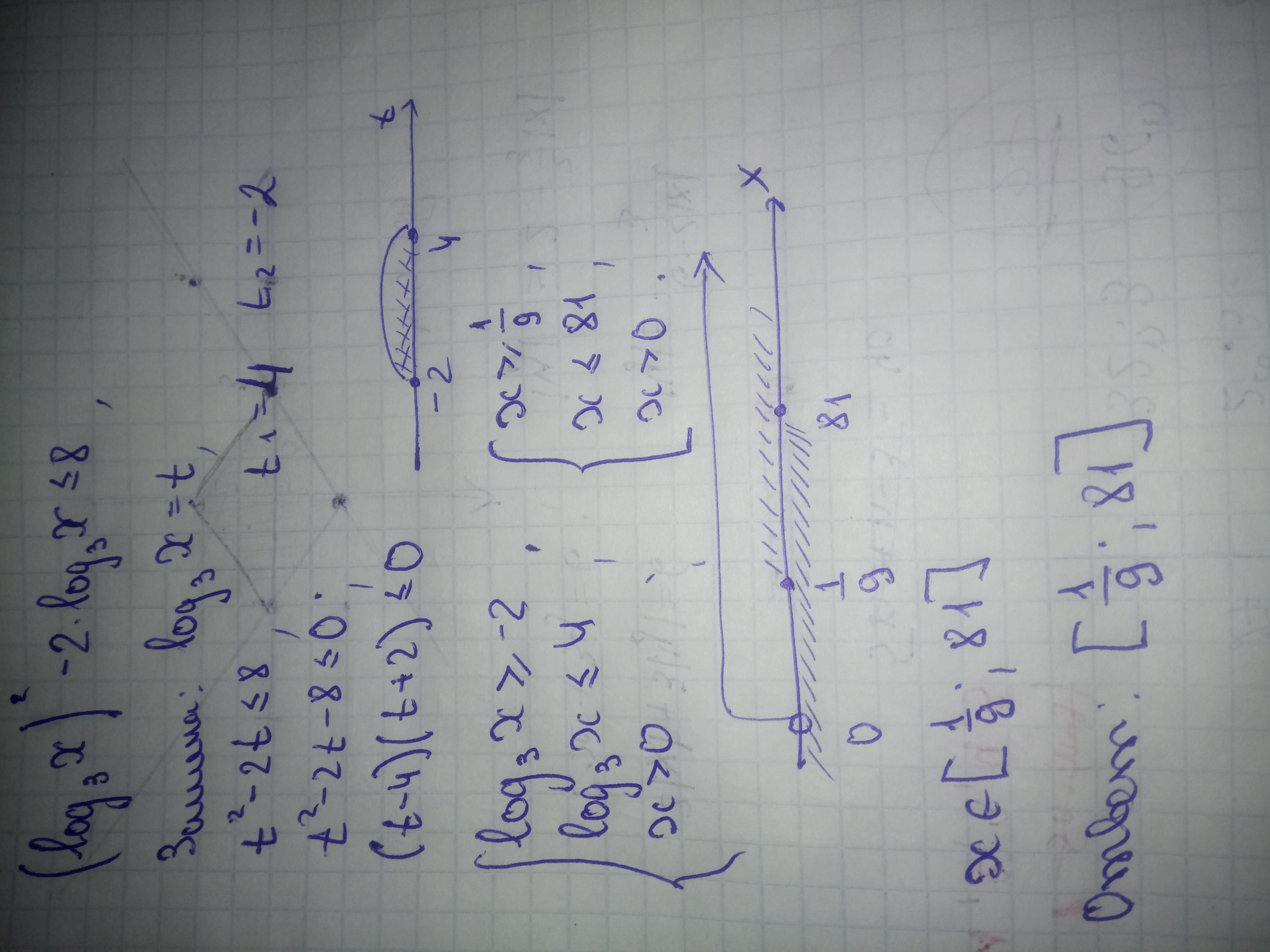
ОДЗ: x >0
Замена переменной:
D=4+32=36 ⇒ t=-2 или t=4
Обратный переход:
Логарифмическая функция с основанием 3 монотонно возрастает, поэтому:
найденные решения входят в ОДЗ
О т в е т.
Автор ответа:
0
Ответ [1/9; 81]
Решение неравенства.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: marinamikhieie
Предмет: Русский язык,
автор: Milashka1995o
Предмет: Русский язык,
автор: natalias8
Предмет: Математика,
автор: zoro199999
Предмет: Математика,
автор: nigorakuldashe