Предмет: Алгебра,
автор: nabizonr51
Найдите сумму всех натуральных значений n, удовлетворяющих неравенству n^2(n^2 - n - 6) ≤ 0
Приложения:
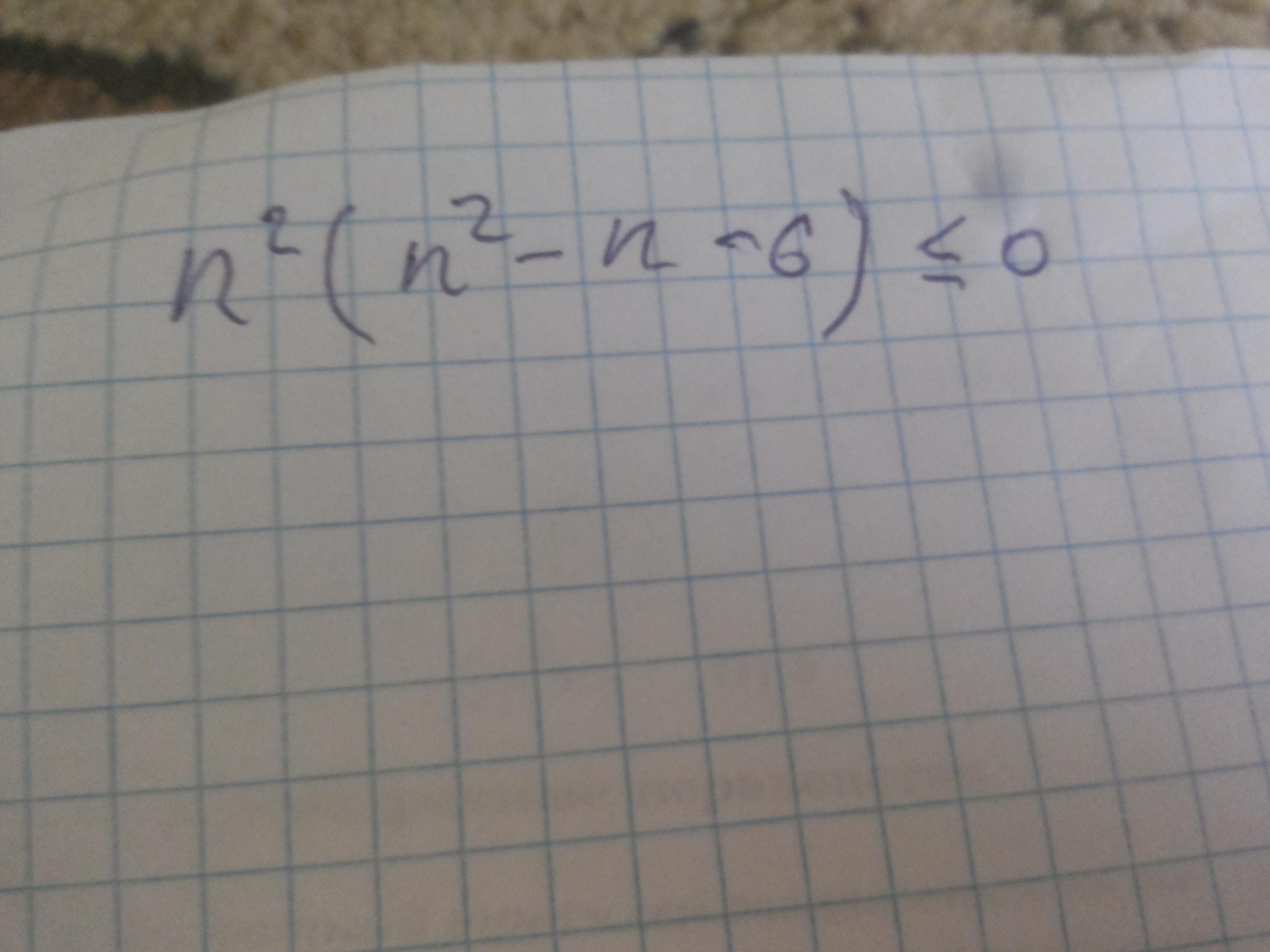
Ответы
Автор ответа:
3
n²(n² - n - 6) ≤ 0
n²(n - 3)(n + 2) ≤ 0
+ - - +
_____[-2]______[0]______[3]_____ n
/////////////////////////////////
n ∈ [- 2 , 3]
Натуральные числа принадлежащие этому отрезку : 1 ; 2 и 3 .
1 + 2 + 3 = 6
Ответ : 6
Автор ответа:
0
n²(n²-n-6)≤0
найдем корни левой части.
n=0; по Виету n=3: n=-2.
____-2_______0___________3____
+ - - +
х∈[-2;3], сумма натуральных, входящих в ответ , 1+2+3=6
Похожие вопросы
Предмет: Русский язык,
автор: sneeook
Предмет: Русский язык,
автор: 1431029
Предмет: Русский язык,
автор: Луна584
Предмет: История,
автор: Valeria18082005Lerka