Предмет: Математика,
автор: sproff
Найдите область значения и область определения функции y = 1/(16x²+49). Правильный ответ на фото(1.13, под буквой а), но я не понимаю, как он был получен
Приложения:
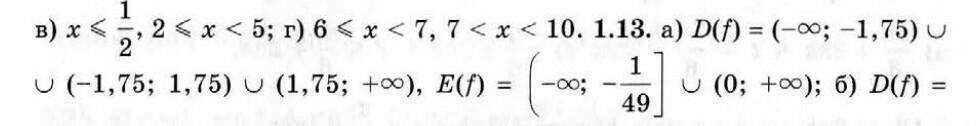
Аноним:
А он неправильный. Если в знаменателе +, то он вообще в нуль не обращается и область определения все числа
А область значений от 0 до 1/49
А где там показано, что он обращается в нуль?
Ответ правильный, проверял в построителе графиков
ответ точно для примера а)? Совсем не для данной функции...
вы можете проверить в построителе графиков
Ну сам напросился
да, всё правильно
Ответы
Автор ответа:
1
Знаменатель всюду положительный, значит область определения функции - вся числовая прямая
Далее заметим что знаменатель больше или равен 49, причем сверху ничем не ограничен. Следовательно, значение функции может быть сколь угодно малым положительным числом, но не превосходящим 1/49 (достигается при x=0)
Значит
Похожие вопросы
Предмет: Русский язык,
автор: ianalegotina
Предмет: Русский язык,
автор: Kopin99
Предмет: Русский язык,
автор: xixxix
Предмет: Математика,
автор: polinasaprykina10