Помогите срочно решить
Ответы
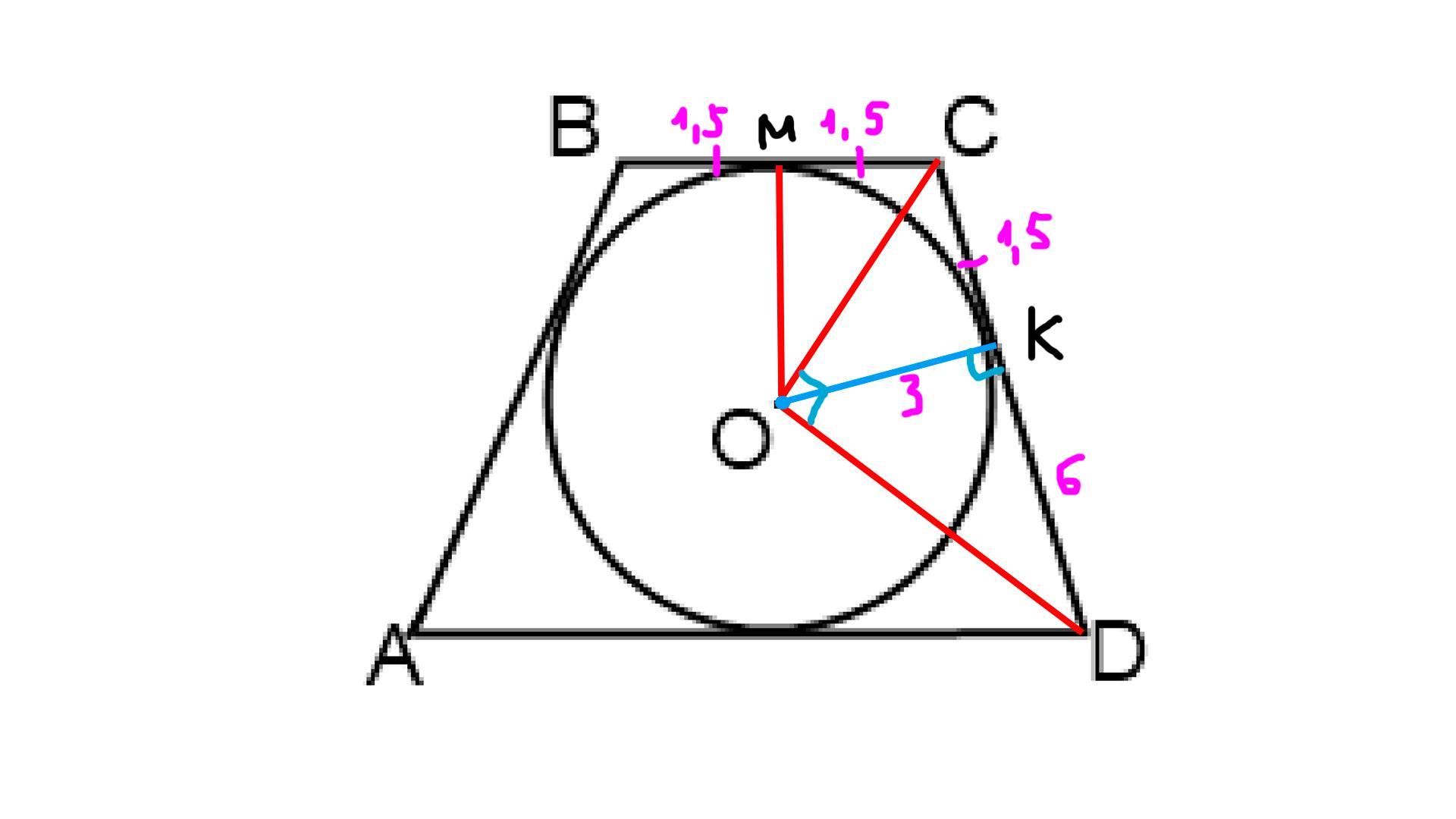
Дано : BC = 3 , 3 = OM = OK - радиусы, окружность с центром О - вписанная.
Найти : AD
-------------------------------------------
1) Радиус OM делил сторону BC на два равных отрезка(т.к трапеция равнобедренная), то есть BM = MC = 3 : 2 = 1.5
2) MC = CK = 1.5 (т.к теорема про касательные к окружности проведенные с одной точки)
3) Рассмотри треугольник COD :
1. Пусть ∠ ADC = x, a ∠BCD = y => ∠ODK = 0.5x, a ∠OCK = 0.5y( т.к OC и OD - биссектрисы, легко доказывается через равенство треугольников)
x + y = 180° (т.к BC || AD)
0.5x + 0.5y = 0.5(x + y) = 0.5 * 180° = 90°
То есть ∠ODK + ∠OCK = 90° => ∠COD = 180° - 90° = 90° => треугольник COD - прямоугольный.
2. По теореме про высоты проведенную к гипотенузе :
CK * DK = OK^2
1.5 * DK = 9
DK = 6
3) AD = 2 * 6 = 12 или по теореме про вписанную окружность в четырехугольник :
3 + x = 2(6 + 1.5)
3 + x = 2 * 7.5
3 + x = 15
x = 12
Ответ : 12 см