Предмет: Математика,
автор: koppod
Решите пожалуйста ИМЕННО с помощью формулы разности синусов. Заранее спасибо.
Приложения:
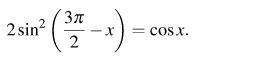
NNNLLL54:
синус разности ...
Ответы
Автор ответа:
1
Спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: zlo159
Предмет: Українська література,
автор: Аноним
Предмет: Русский язык,
автор: dashkachernkova
Предмет: Математика,
автор: Maksim2305