Предмет: Математика,
автор: imaf4194oyby6v
Найдите площадь квадрата ABCD
Приложения:
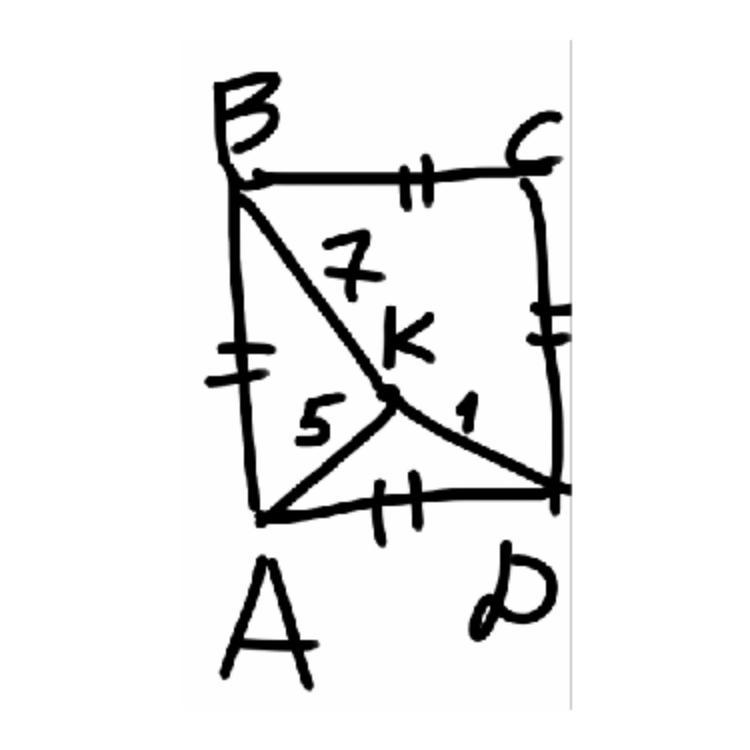
OneGyrus:
Для каких ?
bkd akd akb
их сумма 2pi
Ну это не самое удобное
кому как)
KAB и KAD самое оптимальное
А, ну да.
Что-то я сразу не заметил
Там все сократится и только удвоенные произведения останутся
на косинусы
Ответы
Автор ответа:
1
Ответ: 32
Пошаговое объяснение:
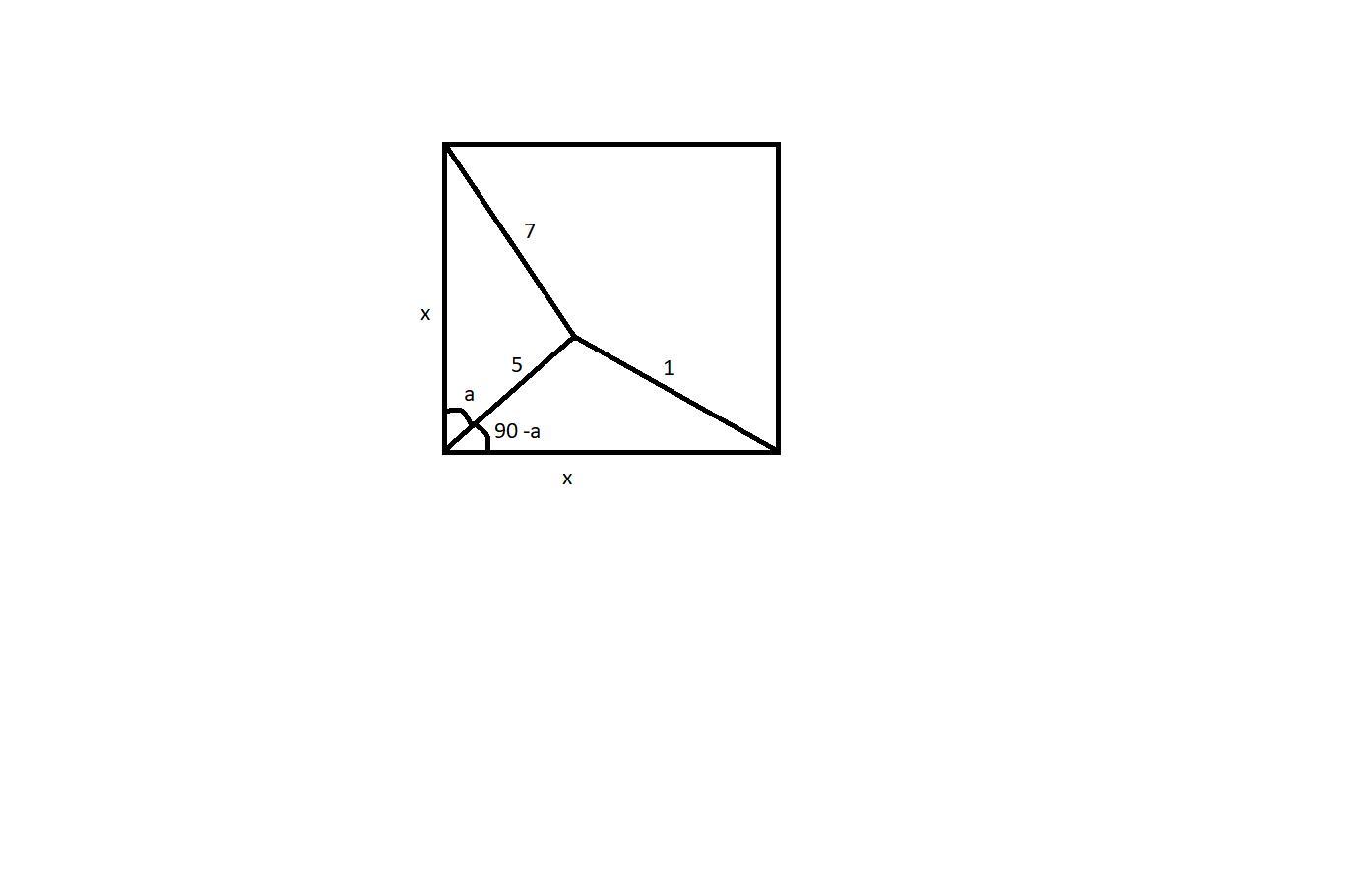
Смотрите рисунок.
Пусть сторона квадрата равна , тогда площадь квадрата
По теореме косинусов, учитывая, что имеем:
Поскольку угол - острый, должно быть выполнено неравенство:
Преобразуем:
Сложим оба уравнения, учитывая основное тригонометрическое тождество:
Таким образом :
Приложения:
Самое интересное, что сами значения размеров, уже говорят, что все таки точка лежит на диагонали. Ибо 7
7+1= 8 , d= корень(32) * корень (2) = 8 , но такое возможно лишь когда треугольник вырожденный
Возможно есть способ хитро доказать, что точка лежит на диагонали, используя неравенства треугольника, но чето как то не получается...
Даже интересно, надо будет завтра подумать.
Есть вариант доказать, что БКД - 180°
Это интересно , если решать без тригонометрии. А так да можно. Должен быть красивый способ при помощи неравенств.
Похожие вопросы
Предмет: Русский язык,
автор: lugansktruba
Предмет: Английский язык,
автор: МалинаЧерника
Предмет: Русский язык,
автор: DashkaChuchundra
Предмет: Геометрия,
автор: ponylol1