Предмет: Математика, автор: danabatchvarova

Для которых n ∈ N имеет различные естественные числа

Приложения:

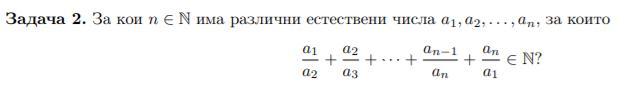
MaxLevs: Для каких n ∈ существуют различные(не равные) числа a1, a2, a3,..., для которых выполняется равенство [...]?

MaxLevs: различные натуральные* числа

MaxLevs: Странная зачада

MaxLevs: Указано, что а1, a2, a3, etc. ∈ , но нигде не сказано, что a1

MaxLevs: что а1 обязательно должен быть = 1, a a2 = 2ю

MaxLevs: Тогда я могу выдрать любые натуральные числа и подставить их, главное, чтобы они выражение делали натуральным числом

Ответы

Автор ответа: Guerrino

Докажем, что для любого $n\geq 3$ существует требуемый набор. Пусть $a_{j}=(n-1)^{j-1}$ . Имеем: $\frac{(n-1)^{0}}{(n-1)^1}+\frac{(n-1)^1}{(n-1)^2}+...+\frac{(n-1)^{n-1}}{(n-1)^0}=(n-1)\times \frac{1}{n-1}+(n-1)^{n-1}=1+(n-1)^{n-1}\in\mathbb{N}$ , причем все $a_{j}$ различны.