Question

пр4) Найдите наибольшую площадь (м^2) земельного участка прямоугольной формы , который можно огородить забором длиной 360 м . ( применяя производную)

Спасибо!​

Answer 1

Сумма длин двух сторон этого прямоугольника равна 180 м. Пусть длина одной стороны равна $x$. Тогда длина второй равна $180-x$. Площадь участка равна произведению длин сторон: $S=x(180-x)$. Рассмотрим эту площадь как функцию, найдём её производную и экстремум:

$f(x)=x(180-x)=180x-x^2\\f'(x)=180-2x$

Приравняем производную к нулю, чтобы найти экстремум:

$f'(x)=180-2x=0\\180=2x\\x=90$

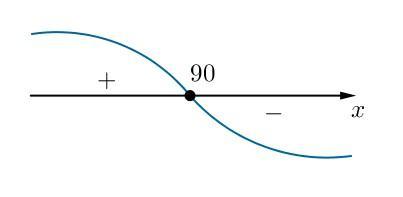
Методом интервалов (см. иллюстрацию) устанавливаем, что при прохождении через точку $x=90$ производная меняет знак с плюса на минус. Это значит, что $x=90$ — точка максимума.

Это означает, что длины сторон этого прямоугольника должны быть равны, то есть это квадрат со стороной длиной 90 м.  Его площадь равна $90^2=8\,100$ м²

Ответ: 8 100 м²