Question

ПОМОГИТЕ пожалуйста!!! Даю 40 баллов Квадрат ABCD, вырезанный из тонкого ровного листа жести, скользит по плоской поверхности. В некоторый момент времени скорость вершины A равна v=1 м/с и направлена к вершине B, а угловая скорость вращения квадрата ω=4 рад/с. Длина стороны квадрата a=25 см. Найдите величины скоростей вершин B, C и D квадрата, если направление обхода вершин квадрата противоположно направлению его вращения. Ответы выразите в м/с, округлите до сотых и введите в порядке возрастания.

Answer 1

Ответ:

$\displaystyle v_B=1.41$ м/с

$\displaystyle v_D=2$ м/с

$\displaystyle v_C=2.24$ м/с

Объяснение:

Примечание: эта задача уже была решена мной 26.07.2020, дублирую сюда свое решение.

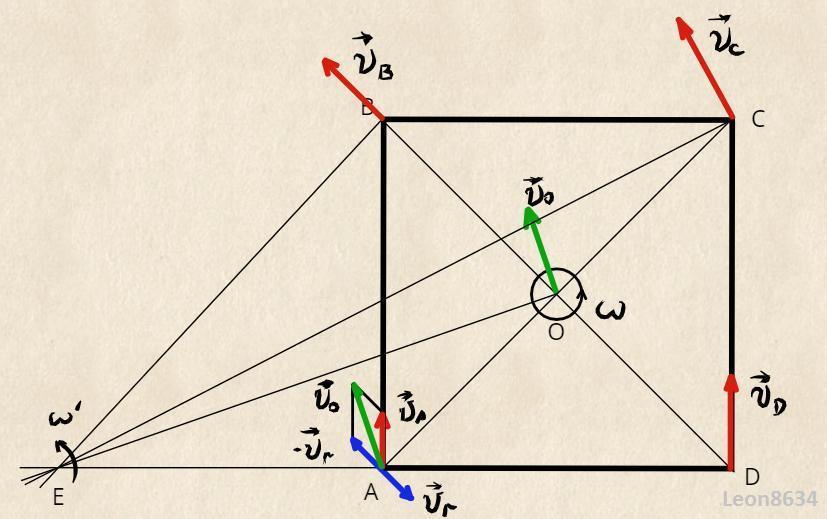
Основная идея решения задачи - вся фигура вращается вокруг некоторой точки, называемой - мгновенный центр скоростей. В нашем случае этой точкой является точка Е. Угловая скорость вращения вокруг этой точки ω' совпадает с угловой скоростью вращения квадрата ω (аналитическое доказательство этого изложено в прошлом решении). Зная это, легко найти скорости вершин квадрата:

$\displaystyle EA=\frac{v_A}{\omega'}=\frac{1}{4}=0.25$ м

$\displaystyle v_D=\omega'ED=4*(0.25+0.25)=2$ м/с

$\displaystyle v_B=\omega 'BE=4*\sqrt{2}*0.25=1.414$ м/с

$\displaystyle v_C=\omega'EC=4*\sqrt{0.25^2+0.5^2}=2.236$ м/с.