Предмет: Математика,
автор: bvv327
решите неравенство 3*49^x-16*21^x+21*9^x <0
Ответы
Автор ответа:
0
Обе части разделим на . Получим:
Замена:
Т.к. стоял знак <, то
ОТВЕТ:
Автор ответа:
1
Ответ:
х>1
Пошаговое объяснение:
решение во вложении ( три фото)
Приложения:

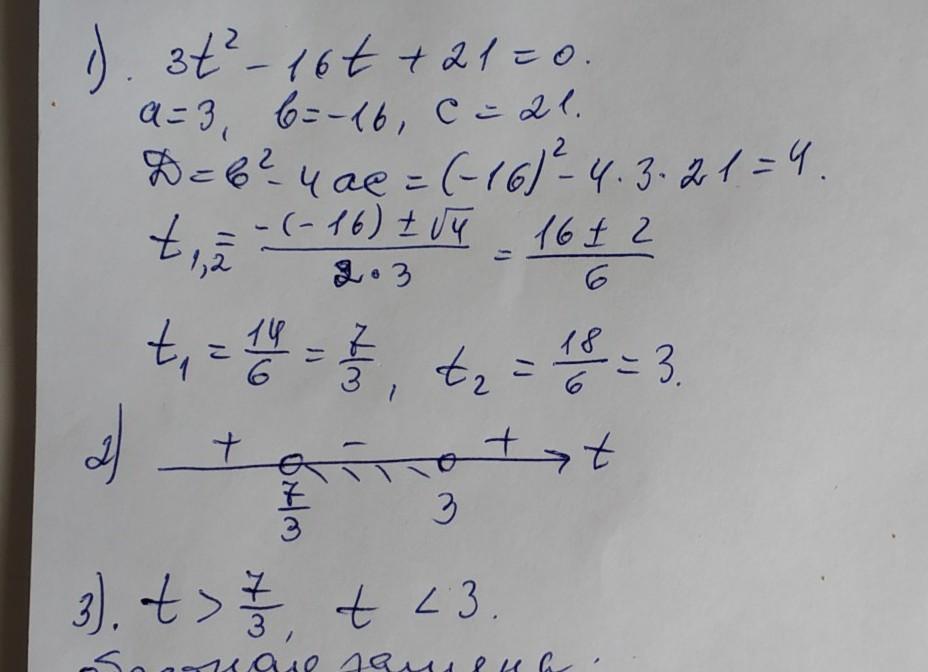

Похожие вопросы
Предмет: Английский язык,
автор: милAna
Предмет: Другие предметы,
автор: Тесса4
Предмет: Русский язык,
автор: nikitaduckarev
Предмет: Литература,
автор: Жала11
Предмет: Математика,
автор: dmitros228