Предмет: Физика,
автор: G00dbye
Помогите с физикой!!!
Приложения:
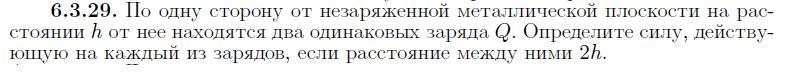
ЮрВас:
!!! Четыре заряда по углам прямоугольника.
Квадрата.
Так и решал, но ответ малость не сходится с ответом в учебнике
Ответы
Автор ответа:
7
Ответ:
или
если учесть что
Объяснение:
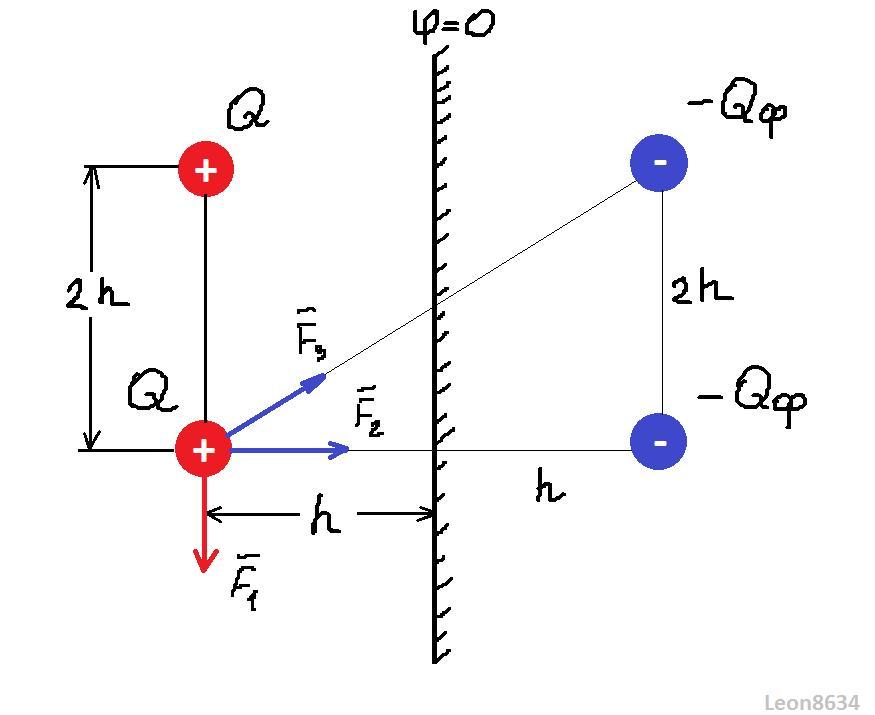
Воспользуемся методом электростатических изображений (см. рисунок). Влияние проводящей плоскости можно заменить на влияние двух фиктивных противоположных зарядов, расположенных на таком же расстоянии по другую сторону плоскости и обеспечивающих равенство нулю потенциала на ее поверхности. Таким образом, на выделенный заряд действуют три силы:
Найдем величину результирующего вектора:
Сумму векторов и
также найдем по теореме Пифагора, приняв во внимание, что угол между векторами 90°:
, на остальные три заряда будет действовать такая же по модулю сила.
Приложения:
Спасибо. Отличное решение, все максимально доступно и понятно
Похожие вопросы
Предмет: Другие предметы,
автор: ПушистаяЛеди
Предмет: Другие предметы,
автор: ПушистаяЛеди
Предмет: Английский язык,
автор: Lenavladykina
Предмет: Физика,
автор: Salamandra200
Предмет: Информатика,
автор: Ramazankashkimb