Question

Площа прямокутника ABCD дорівнює 12 см^2. Знайти площу AОB. О – точка перетину діагоналей.​

Answer 1

Ответ:

(см. объяснение)

Пошаговое объяснение:

1-ый способ:

Заметим, что диагонали прямоугольника делят его на 4 равновеликих треугольника. Это получается из-за того, что диагонали прямоугольника точкой пересечения делятся пополам, и синусы смежных углов равны. Тогда $S_{AOB}=\dfrac{S}{4}=3$.

2-ой способ:

Площадь прямоугольника можно вычислить по формуле $S=\dfrac{d^2}{2}\times\sin a$, откуда $\sin a=\dfrac{2S}{d^2}$. Площадь треугольника AOB вычисляется по формуле $S_{AOB}=\dfrac{d^2}{8}\times\sin a$. Подставим выраженный выше $\sin a$ в полученную формулу: $S_{AOB}=\dfrac{d^2}{8}\times \dfrac{2S}{d^2}=\dfrac{S}{4}$. Тогда $S_{AOB}=\dfrac{12}{4}=3$.

Задача решена!

Answer 2

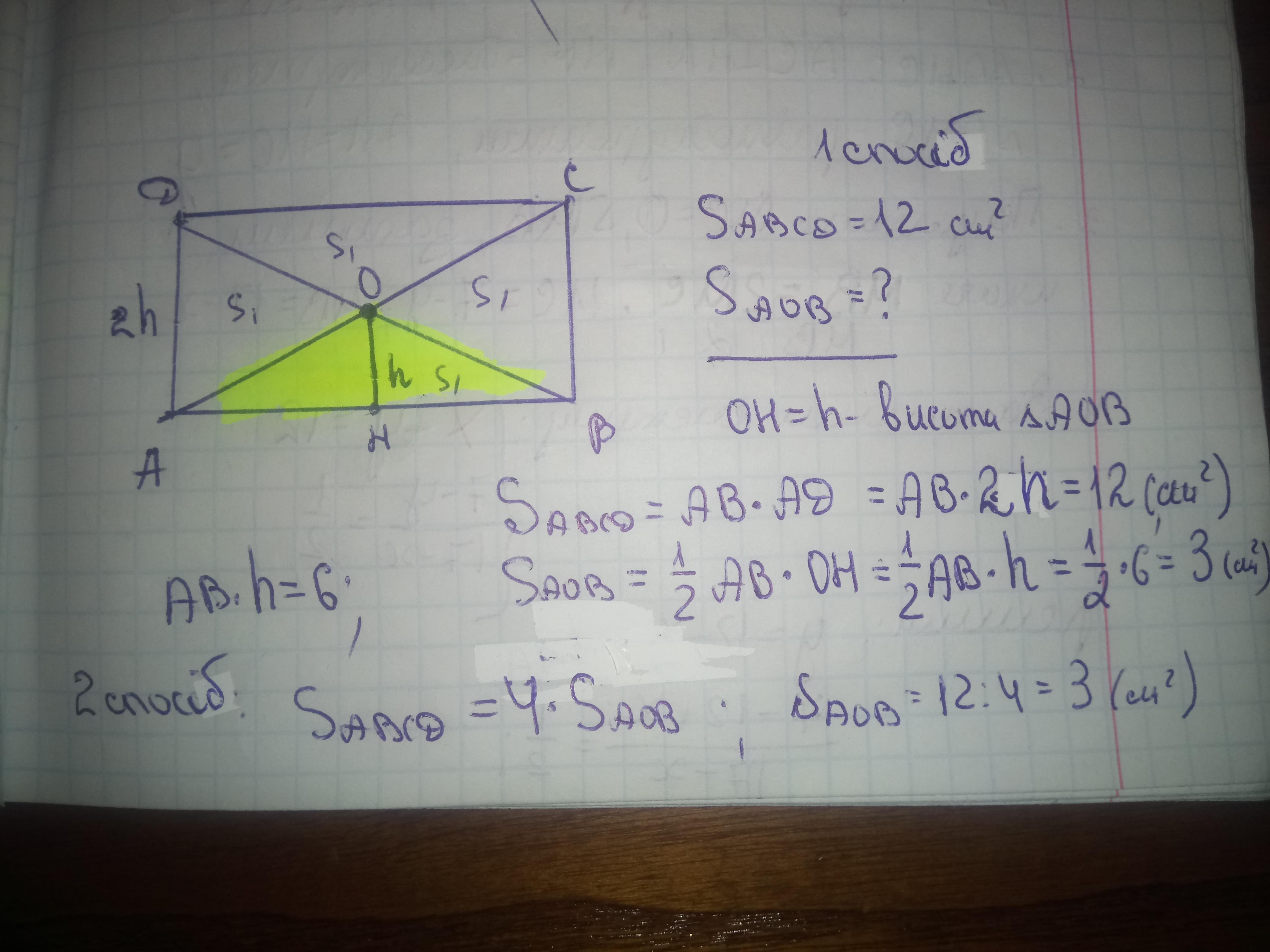
Відповідь : 3 см2

Розв'язання завдання додаю