Предмет: Алгебра,
автор: StellaICH
Алгебра 8 класс. ПОЖАЛУЙСТА С ОБЪЯСНЕНИЕМ!
Приложения:
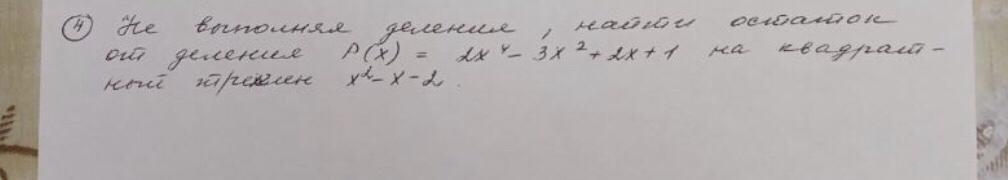
Ответы
Автор ответа:
2
Дано:
Найти - остаток от деления
Решение.
1) Для начала разложим многочлен на множители, для этого решим уравнение:
2) Так как данный многочлен делится на
с остатком, то представим его в виде
где
- неполное частное;
- искомый остаток.
Степень остатка деления многочлена на многочлен должна быть меньше степени делителя. В данном случае делитель - многочлен второй степени, так что остаток - многочлен первой степени, который имеет вид:
3) Подставим в равенство первый корень
и получим:
Вычислим .
Так как , то
=>
4) Аналогично решаем и со вторым корнем .
5) Подставим в полученное уравнение:
6)
- искомый остаток.
Ответ:
Khadgar1111:
так деление есть
Деления данных многочленов в столбик в решении нет!
Похожие вопросы
Предмет: Русский язык,
автор: kojokaru
Предмет: Английский язык,
автор: Alenyshka18
Предмет: Русский язык,
автор: naniten
Предмет: Литература,
автор: KimCat
Предмет: Алгебра,
автор: ksymill