Предмет: Алгебра,
автор: MaxCybertron
Даю 10 балов за 2 задачи
Приложения:
Ответы
Автор ответа:
1
Ответ:
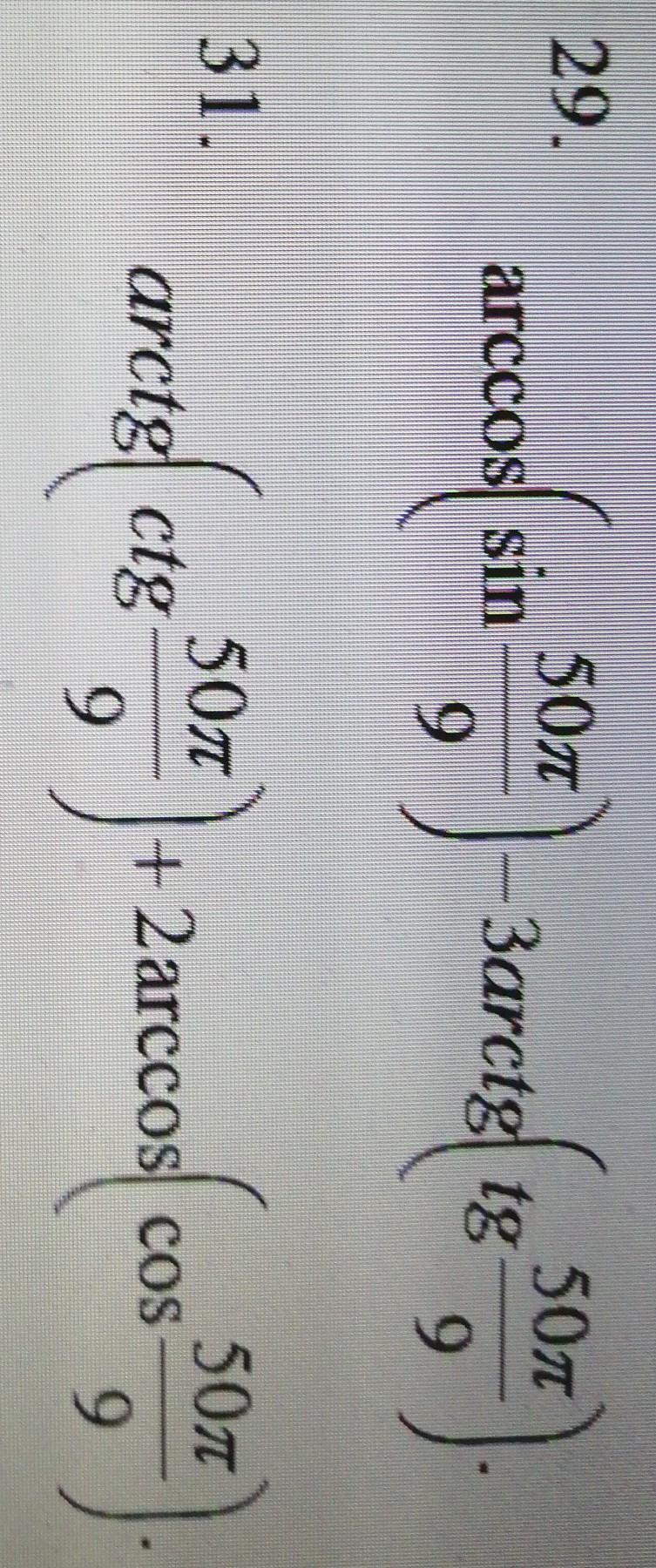
№29: 41π/18
№31: 5π/6
Объяснение:
воспользуемся формулами приведения:
Также воспользуемся :
№29
Воспользуемся свойством периодичности косинуса:
cosx=cos(x+2πk), k∈Z
Значит:
также поступаем с тангенсом:
tgx=tg(x+πk), k∈Z
Значит:
Таким образом:
№31
Так как косинус - это четная функция, значит cos(-x)=cosx
MaxCybertron:
А почему должны быть условия [0;п] и (-п/2;п/2)?
это области значений для обратных тригонометрических функций
точно также как и синус не может быть больше 1 или меньше -1
а для арксинуса и арккотангенса такие же области?
для арксинуса [-pi/2;pi/2]. Для арккотангенса (0; pi)
Спасибо большое
Похожие вопросы
Предмет: Қазақ тiлi,
автор: jkzgjgdf
Предмет: Русский язык,
автор: Lalak12
Предмет: Русский язык,
автор: lenakrjar
Предмет: Математика,
автор: loginbaklina20