Предмет: Алгебра,
автор: malta12
Все корни равенства в этой промежутке.
Приложения:
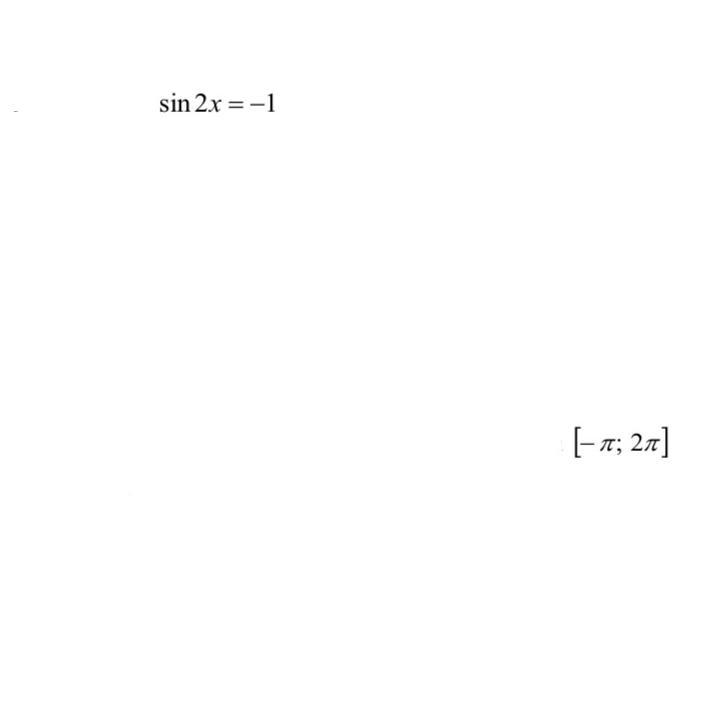
Ответы
Автор ответа:
3
Решение:
Ответ:
Примечание:
В решении мы использовали, что значение синуса становится равным в точках
.
Также, уравнение решается в общем случае вот так:
.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Пoлuнa
Предмет: Қазақ тiлi,
автор: мадина092000
Предмет: Литература,
автор: Ulyana7covyhka
Предмет: Физика,
автор: Блоди1