Предмет: Алгебра,
автор: Mirmars
Найдите площадь области, заданной неравенством. Если можно с подробным решением
Приложения:

Ответы
Автор ответа:
0
Объяснение:
|x-2|+|y+3|≤1
ОДЗ:
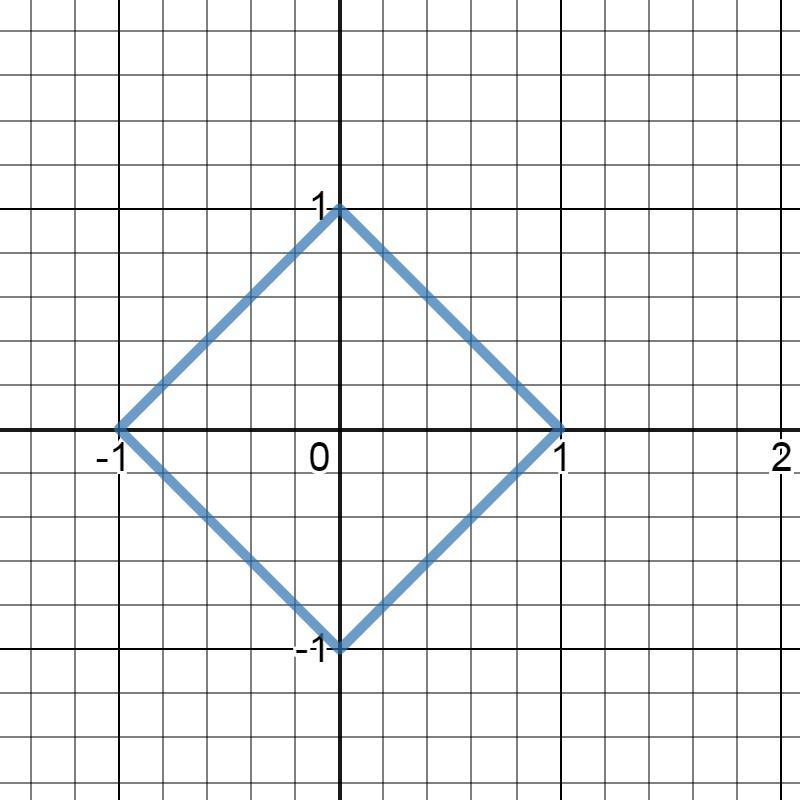
Сначала построим график функции |x|+|y|=1.
Первый квадрант (первая четверть):
Второй квадрант:
Третий квадрант:
Четвёртый квадрант:
Таким образом, график выглядит следующим образом (см. рис.1)
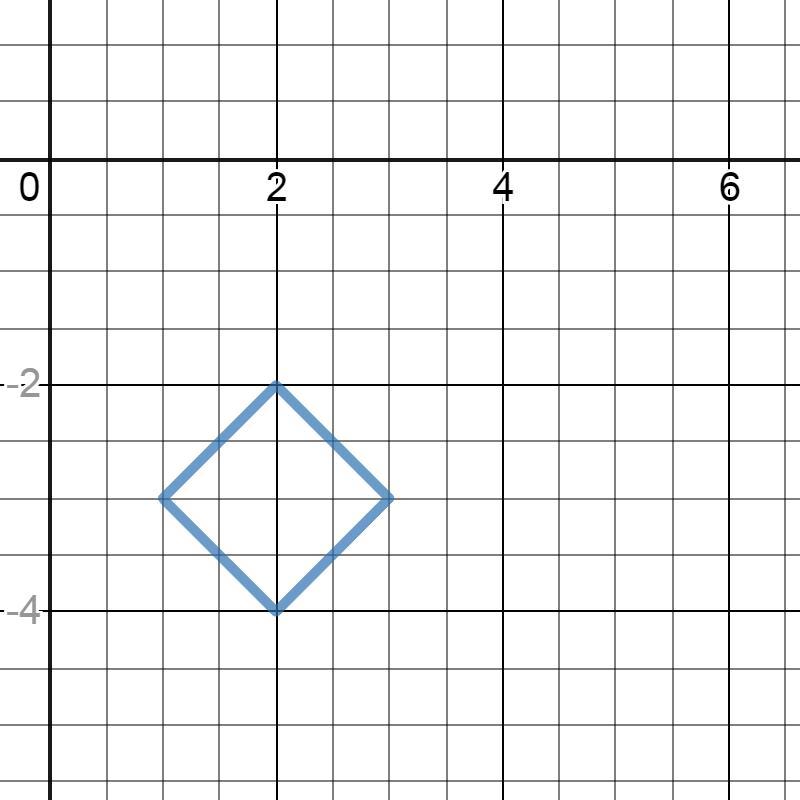
График |x-2|+|y+3|=1 - график функции |x|+|y|=1, смещённый вправо по оси ОХ на две единицы и опущенный вниз по оси ОУ на три единицы.
(см. рис 2).
Исходя из ОДЗ площадь области, заданная неравенством |x-2|+|y+3|≤1
находится внутри квадрата со стороной = √(1+1)=√2 (клетки). ⇒
Площадь данного квадрата = (√2)²=2 (кв. клетки).
Ответ: площадь области, заданная неравенством |x-2|+|y+3|≤1
равна 2 кв. клетки.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: 14012013
Предмет: Другие предметы,
автор: katyanikolaeva0465
Предмет: Другие предметы,
автор: sonya232
Предмет: Химия,
автор: Shayrm