Question

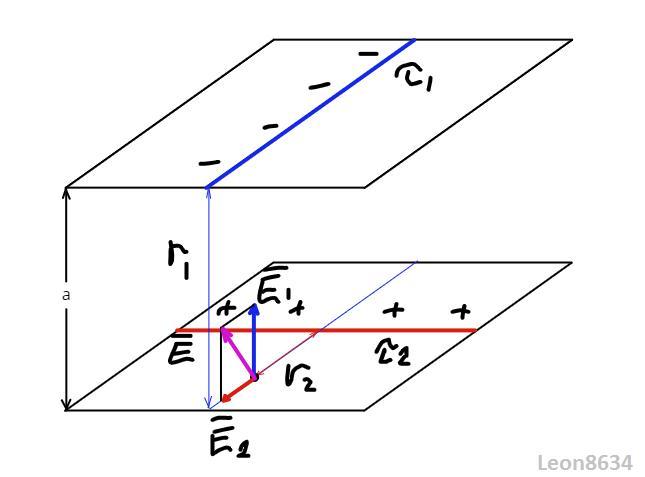
Электрическое поле создано двумя заряженными бесконечными нитями,
лежащими в параллельных плоскостях и скрещенных под прямым углом. Линейные
плотности зарядов ништей равны: T=-0.2мкКл/м. 2=0,02мкКлім. Найти
напряженность поля в точке, расположенной на расстоянии r =13см от первой и
r, =5см от второй нити. Расстояние между нитями а=13см.​

Answer 1

Ответ:

28600 В/м

Объяснение:

Напряженность поля, создаваемого бесконечной заряженной нитью (выводится на основании теоремы Гаусса):

$\displaystyle E=\frac{\tau}{2\pi \epsilon_0r}$

Рассчитаем напряженности от первой и второй нитей:

$\displaystyle E_1=\frac{\tau_1}{2\pi \epsilon_0r_1}=\frac{-0.2*10^{-6}}{2*3.14*8.85*10^{-12}*0.13}=-27680$ В/м, направлена к нити

$\displaystyle E_2=\frac{\tau_2}{2\pi \epsilon_0r_2}=\frac{0.02*10^{-6}}{2*3.14*8.85*10^{-12}*0.05}=7197$ В/м направлена от нити

Результирующую напряженность поля найдем по теореме Пифагора:

$\displaystyle E=\sqrt{E_1^2+E_2^2}=\sqrt{(-27680)^2+7197^2}=28600$ В/м.

Примечание: На самом деле у этой задачи бесконечно много решений, все точки, удовлетворяющие условию задачи, лежат на кривой пересечения двух цилиндров (см. рисунок). Мы выбрали самую очевидную и простую для расчета точку, она помечена фиолетовым.