Решите уравнение, нужна теорема Коши
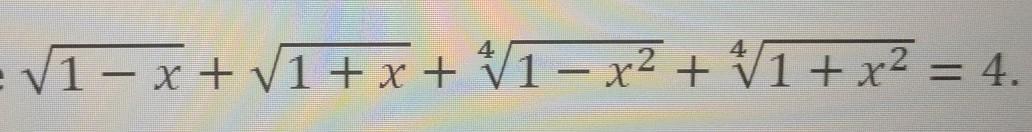
Ответы
Посмотрите такое решение. Прошу и остальных посмотреть и дать комментарии.


Обозначим функцию в левой части равенства как
Понятно, что (т.е. она четная) и что
определена на интервале
Это все упрощает. Самый элегантный способ решения - разложить функцию слева в ряд Маклорена (табличные корни с нужной областью определения, за исключением точек -1 и 1, которые вручную проверяются)
Сразу ясно, что функция имеет единственное пересечение с четверкой.
Но если по школьному, то надо взять производную:
Далее понятно, что при приближении к точке 1 знаменатели отрицательных дробей стремятся к нулю, а значит эти отрицательные составляющие стремятся к бесконечности. На интервале от 0 до 1 производная ф-ии отрицательна, значит функция монотонно убывает.
В силу четности, на интервале от -1 до 0 она будет монотонно возрастать. Ясно, что является максимумом, тогда просто посчитав
имеем право заключить, что уравнение имеет единственное решение: