Предмет: Алгебра,
автор: sfefok
Помогите решить пожалуйста. Срочно надо. Не понимаю как решается.
Полностью с объяснениями пожалуйста
Приложения:
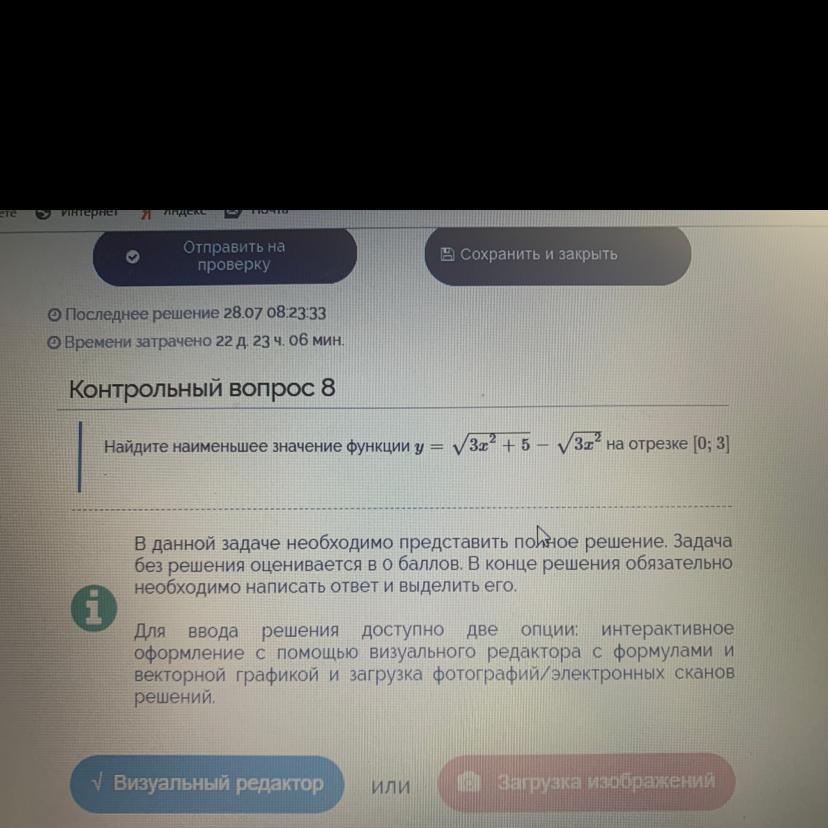
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Заметим, что при x > 0
Значит, при 0 < x ≤ 3 функция убывает, на данном промежутке её наименьшее значение равно .
Отдельно проверим x = 0, так как он не был включён в промежуток: . Сравним f(0) и f(3): заметим, что
. Значит, наименьшее значение функции равно
Похожие вопросы
Предмет: Английский язык,
автор: SGgk
Предмет: Русский язык,
автор: OбPyB0k
Предмет: Русский язык,
автор: AlsuNurtdinowa
Предмет: Математика,
автор: люба294
Предмет: Математика,
автор: АленкаИлюшка