Решить тригонометрическое уравнение: 
Ответы
Раскрываем знак модуля:
Если cosx >0, то |cosx|=cosx
уравнение принимает вид:
По формуле произведения синуса на косинус:
тогда
По формуле разности синусов:
⇒
⇒
⇒
или
⇒
⇒
и
⇒
⇒
и
⇒
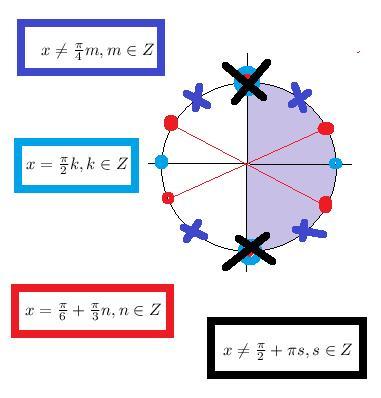
О т в е т первого случая c учетом cosx >0:
( см. рис.1)
Если cosx <0, то |cosx|= - cosx
уравнение принимает вид:
По формуле синуса двойного угла
тогда
⇒
⇒
⇒
или
⇒
или
так как
⇒
и
⇒
⇒
и
⇒
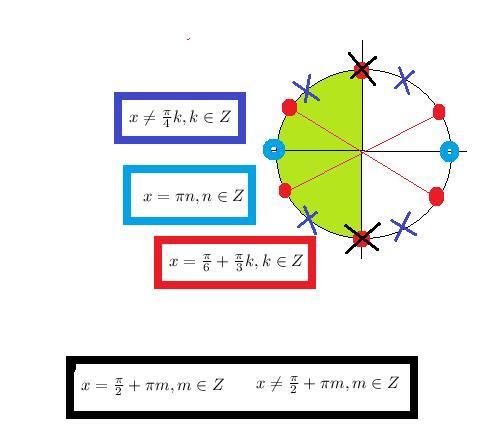
О т в е т второго случая c учетом cosx <0
( см. рис.2)
О т в е т. Объединяем ответы первого и второго случаев: