Предмет: Математика,
автор: Migma11
Найдите

если

(x>0).
vlad97ua:
Надеюсь, что условие верное, потому что на ум ничего не приходит...
условие верное
Ответы
Автор ответа:
1
Ответ:2
Пошаговое объяснение:
Приложения:
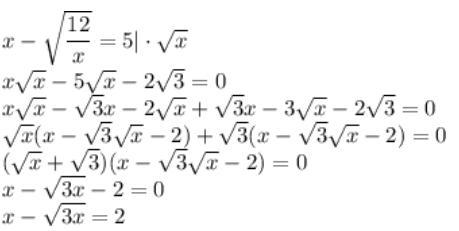
не читается
Прикольно, правда не совсем понятно, как додуматся до превращений в 3 строке, что бы вышли одинаковые множители...
пожалуйста перепишите , у меня не читается
Легко же
xD
Раскрываю секрет как догадаться
Замечаете, что уравнение верно при sqrtx=-sqrt3
И пытаетесь довести до соответствующего множителя
Похожие вопросы
Предмет: Українська мова,
автор: Taras24
Предмет: Русский язык,
автор: legushkamarb
Предмет: Русский язык,
автор: АлександраЯ
Предмет: География,
автор: Akhmedyanovaa1
Предмет: Математика,
автор: котейка58696