Предмет: Алгебра,
автор: anikaarustamova
РЕШИТЕ, ПОЖАЛУЙСТА, УРАВНЕНИЕ! (я сама решила, но мне срочно нужно с кем-нибудь свериться)
Приложения:
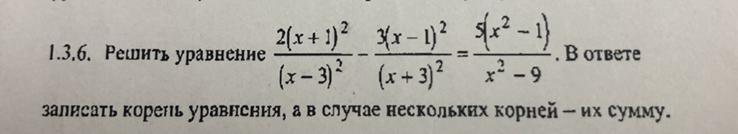
x₁+x₂=8
Ответы
Автор ответа:
1
Замена:
1)
2)
Сумма корней уравнения:
Так, у меня ошибка
Я сейчас переделаю по-быстрому
У меня почему-то в ответе вообще получился только ноль
Ну вы пока на мой ход решения посмотрите... Я сейчас переделаю, я там минус забыл, когда дискриминант считал...
Переделал, теперь вроде всё хорошо
Спасибо огромное, теперь все понятно)
Автор ответа:
0
Всё то же, но с другой заменой
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: madamliza2002
Предмет: Другие предметы,
автор: mterentevagana
Предмет: Русский язык,
автор: Didiana2001
Предмет: Математика,
автор: AnyutkaKim1212
Предмет: Химия,
автор: princess232
x₂=4+√13