Предмет: Алгебра,
автор: kefgekiz
докажите тождество....
Приложения:
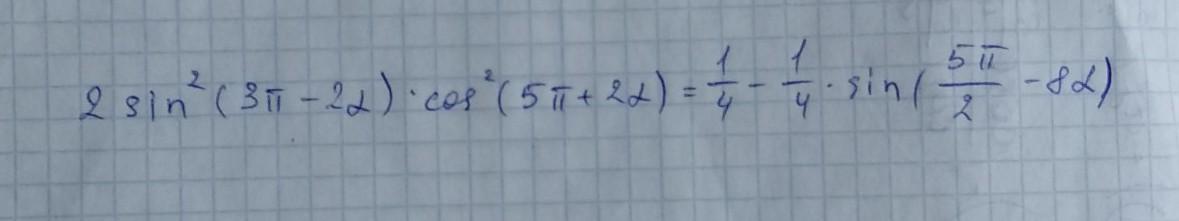
Ответы
Автор ответа:
1
Автор ответа:
2
Добрый день!
Тождество доказано!
Формулы применяемые в решении:
Если решение понравилось, ставь лучший ответ!
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: vchichikina2013
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: Камария
Предмет: Математика,
автор: khristova273