Предмет: Математика,
автор: РиНаБоГ
В скольких МАКСИМАЛЬНЫХ точках могут пересекаться 3 окружности ?
1. 6
2. 5
3. 3
4. 7
5. 4
ОТВЕТ С РЕШЕНИЕМ И ПОЯСНЕНИЕМ
Ответы
Автор ответа:
5
Ответ:
6
Пошаговое объяснение:
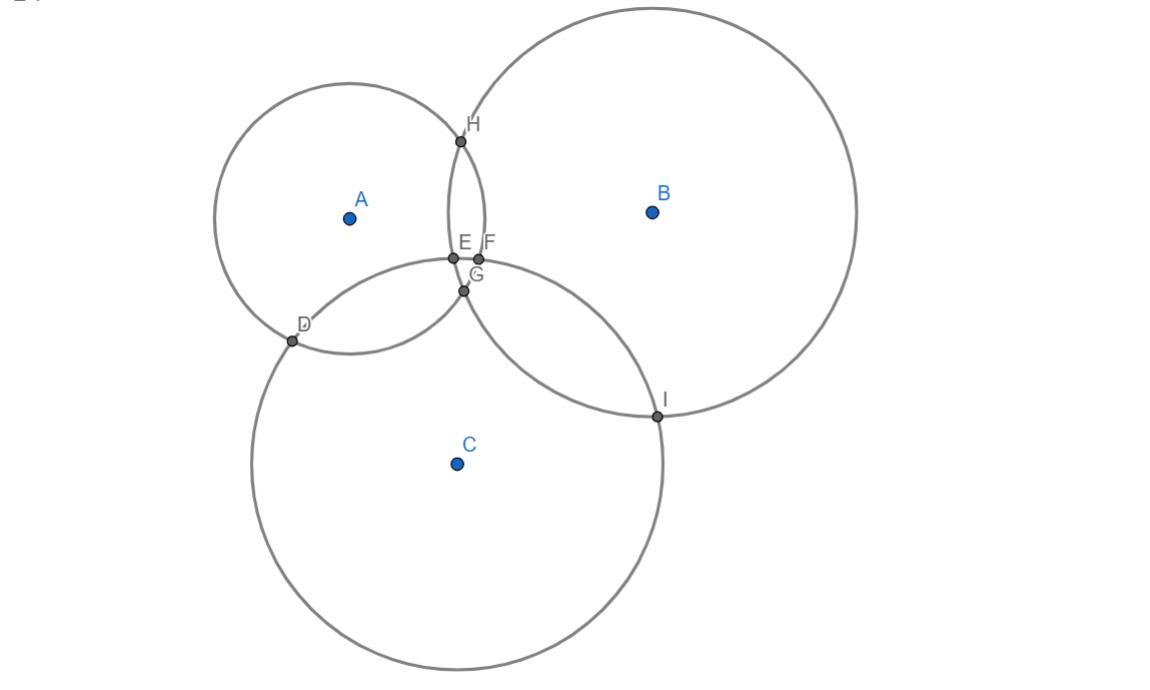
Если две окружности не совпадают, то они пересекаются максимум в двух точках, так как у нас 3 окружности, то есть 3 пары окружностей, значит всего точек пересечения <=3*2 = 6, то есть точек пересечения не больше 6
Пример на 6 точек пересечения (D,E,F,G,H,I):
Приложения:
РиНаБоГ:
Прости, но ответ не 6. У тебя хорошие объяснения и картинка. Но при проверке показало ошибку. Значит решение не верно.
Можете тогда, пожалуйста, найти ошибку в решении
Я сама решила также. И ответила 6. Но ответ оказался неверный. Поэтому и задала вопрос сюда. Значит у вас тоже что то не правильно.
а ошибка не может быть заложена в проверяющей системе
Я проходила электронный тест. Повторно такой же вопрос может не попасться чтобы я проверила другие варианты. Поэтому и не знаю что делать. Может кто то еще сможет это решить? Может тут нужна формула которой я не помню ?
Но всё равно спасибо за отличный ответ!!! Не многие так отвечают :))
просто если ответ больше 6, то между двумя окружностями хотя бы 3 точки пересечения, в это я не верю, поэтому я думаю, что ошибка именно заложена в тесте
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: anzhelaevstifee
Предмет: Русский язык,
автор: svetlanka20
Предмет: Литература,
автор: МаринаГорелова