Предмет: Геометрия,
автор: kalabukhov
помогите пожалуйста Найдите площадь четырехугольника, вершины которого имеют координаты (1;-6), (4;-7), (3;-4), (0;-3).
Ответы
Автор ответа:
1
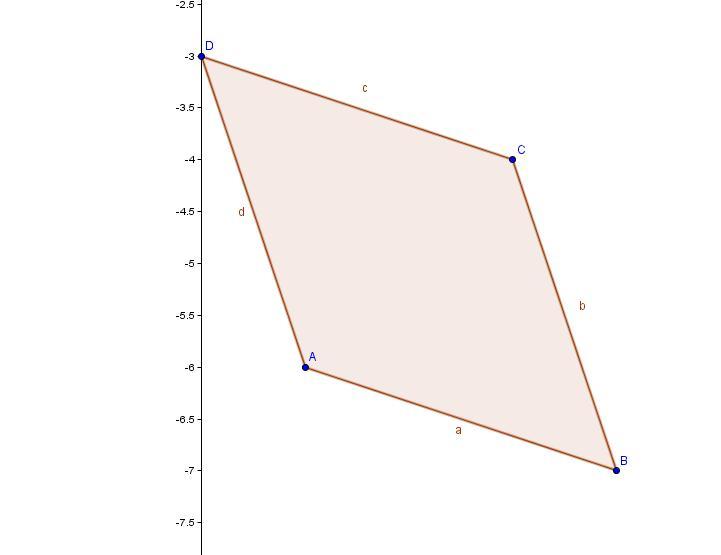
Даны координаты вершин четырехугольника (1;-6), (4;-7), (3;-4), (0;-3).
Проще всего разделить его на 2 треугольника.
Находим длины сторон.
AB (c) = √((xB-xA)² + (yB-yA)²) = √10 = 3,16227766
BC (a) = √((xC-xB)² + (yC-yB)²) = √10 = 3,16227766
AC (b) = √((xC-xA)² + (yC-yA)²) = √8 = 2,828427125
CD = √((xD-xC)² + (yD-yC)²) = √10 = 3,16227766
AD = √((xC-xA)² + (yC-yA)²) = √10 = 3,16227766 .
Площади по Герону.
Периметр Р(АВС) = 9,152982445
Полупериметр р = 4,576491223 .
Площадь S(АВС) = 4,576491223 1,414213562 1,748064098 1,414213562 = √16 = 4
S(ACD) = 4,576491223 1,748064098 1,414213562 1,414213562 = √16 = 4 .
Ответ: S(ABCD) = 4 + 4 = 8 кв.ед.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: fedosjulia
Предмет: Русский язык,
автор: yarginakaty
Предмет: Информатика,
автор: klux
Предмет: География,
автор: Аноним