помогите пожалуйста ( с чертежом)

Ответы
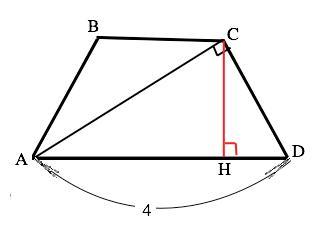
Диагональ ВС равнобедренной трапеции АВСD перпендикулярна стороне СD. Найдите АВ, если AD=4, АВ²+ВС²=11
Ответ: √2
Объяснение: Для удобства записи решения примем АВ=а, ВС=b
Из вершины С проведем к AD высоту СН трапеции.
Высота равнобедренной трапеции делит большее основание на отрезки, из которых меньший равен полуразности оснований, а больший - их полусумме.
Больший отрезок АН= (4+b)/2,, меньший DH=(4-b)/2
Треугольник АСD - прямоугольный ( дано).
В прямоугольном треугольнике высота, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу. => СН²=АН•DH.
СН²=[(4+b)/2]•[(4-b)/2]=(16-b²)/4
В прямоугольном ∆ СНD гипотенуза СD=AB=a
а²=CH²+DH²=(16-b²)/4+ ((4+b)/2)², откуда а²=8-2b
По условию АВ²+ВС²=11 ⇒
а²+b²=11.
Подставим найденное значение а² в это уравнение:
8-2b+b²=11 ⇒ b²-2b-3=0
Решив квадратное уравнение, получим два корня: b₁=3 и b₂=-1. Отрицательный корень не подходит. ⇒ ВС=3
АВ²+3²=11
АВ²=2 => AB=√2