Предмет: Алгебра,
автор: manuvaad
Каким образом можно найти корни в данном равенстве?
Приложения:
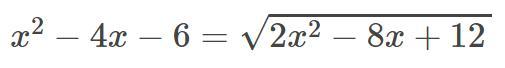
Ответы
Автор ответа:
1
Ответ:
-2; 6
Объяснение:
Уравнение решено!
Похожие вопросы
Предмет: Русский язык,
автор: Michael002
Предмет: Русский язык,
автор: marinafebruary
Предмет: Русский язык,
автор: аринка11111
Предмет: Физика,
автор: РэйнаЭддерри
t = sqrt(2t + 24)
t >= 0