Предмет: Алгебра,
автор: anikaarustamova
ПОМОГИТЕ, ПОЖАЛУЙСТА! ОТДАЮ ПОСЛЕДНИЕ БАЛЛЫ!
В уравнении 19 получается 2 решения:
х=-arctg4+пn
x=п/3+пn
Как понять, принадлежит ли какой-нибудь корень из первого решения (с арктангенсом) отрезку [п/3; 2п/3]
Приложения:
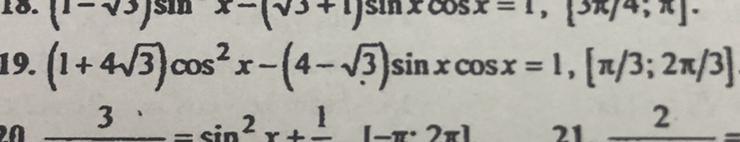
NNNLLL54:
arctg4 є [ п/3;2п/3 ] , но ( -arctg4) не є [ п/3;2п/3 ]
Но при если n=1, то х=-arctg4+п. В этом случае, я не знаю сколько это градусов и не понимаю, принадлежит ли этот корень заданному отрезку
х= -arctg4+П - это уже больше 180 градусов, а промежуток задан [60 ;120] в градусах --> значит не входит этот угол в заданный промежуток.
по таблицам: (-arctg4)=~ (-76) градусов
извиняюсь? всё вышенаписанное для x=+arctg4+П... А если с минусом, то х= -arctg4+П є [П/3;2П/3]
Ответы
Автор ответа:
1
Арктангенс 4 явно больше чем пи/3, потому что тангенс пи/3 это только корень из трех. Ну и как любой арктангенс, он меньше чем пи/2
Значит число "пи-arctg4" лежит между пи/2 и 2пи/3, и разумеется, принадлежит указанному отрезку.
Спасибо огромное, теперь понятно
Автор ответа:
2
Ответ:
Смотри рисунок.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: anya110280
Предмет: Русский язык,
автор: firuza3009
Предмет: Английский язык,
автор: mmalinova2013
Предмет: Математика,
автор: 15НаДеЖдА15
Предмет: Химия,
автор: Аноним