Дан правильный многоугольник и длина радиуса R окружности, описанной около многоугольника. Определи площадь многоугольника, если: - у многоугольника 8 сторон и R= 4 см (если корня в ответе нет, под знаком корня пиши 1). S= ⋅ −−−−−√ см2; - у многоугольника 9 сторон и R= 4 см (ответ округли до целых). S= см2.

Ответы
Ответ:
см²;
см².
Объяснение:
у многоугольника
сторон и
см.
- Число сторон в многоугольнике равно числу углов в этом многоугольнике.
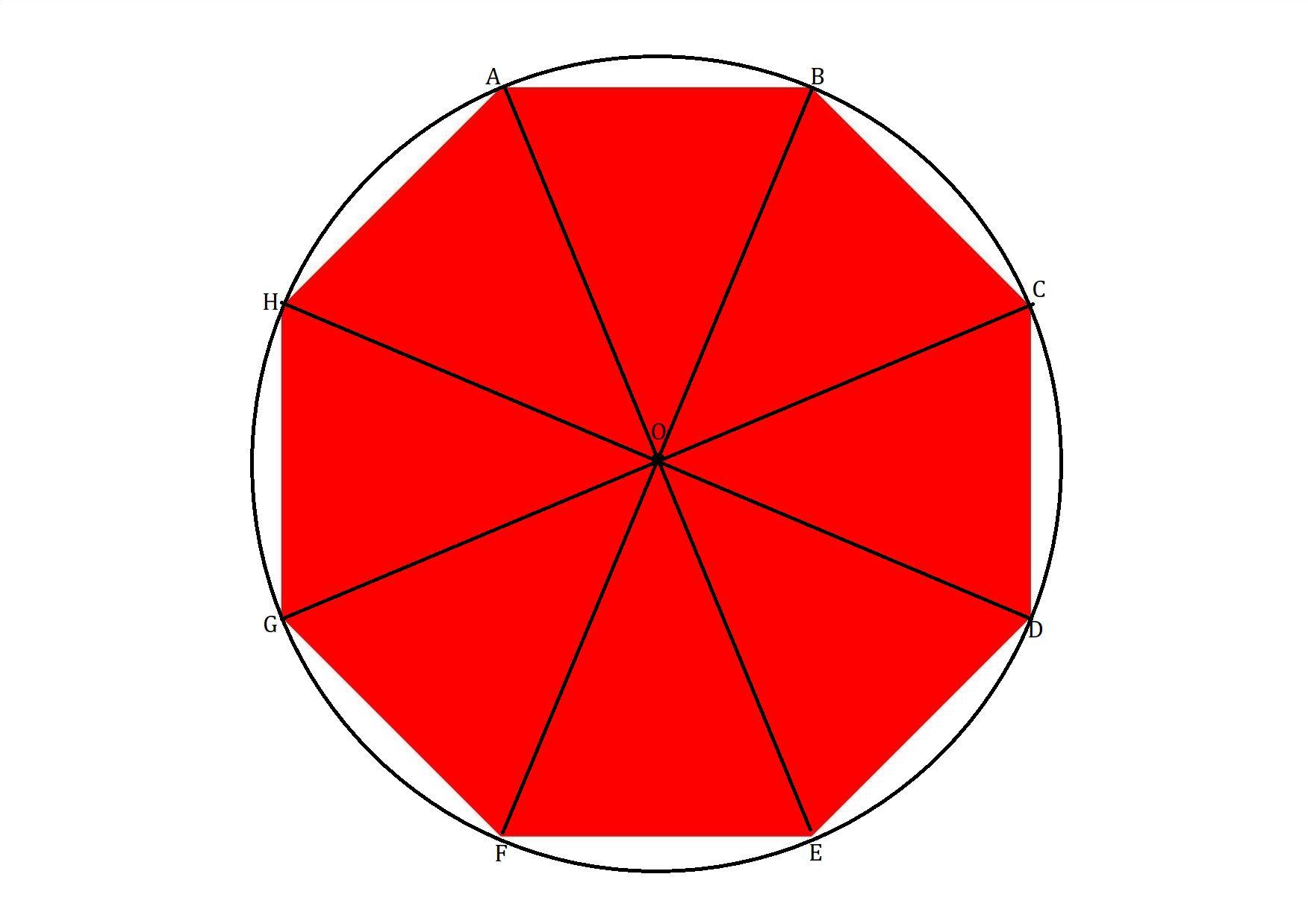
данный многоугольник - восьмиугольный.
Обозначим данный восьмиугольник буквами .
Около восьмиугольника описана окружность с центром в точке
, по условию.
Проведём диагонали .
так как они радиусы описанной около шестиугольника окружности.
- Диагонали правильного восьмиугольника делят его на
равных равнобедренных треугольников.
(а они ещё и равнобедренные).
по свойству равнобедренного треугольника. Также эти стороны - радиусы описанной около данного восьмиугольника окружности.
см²
восьмиугольника =
см².
у многоугольника
сторон и
см.
- Число сторон в многоугольнике равно числу углов в этом многоугольнике.
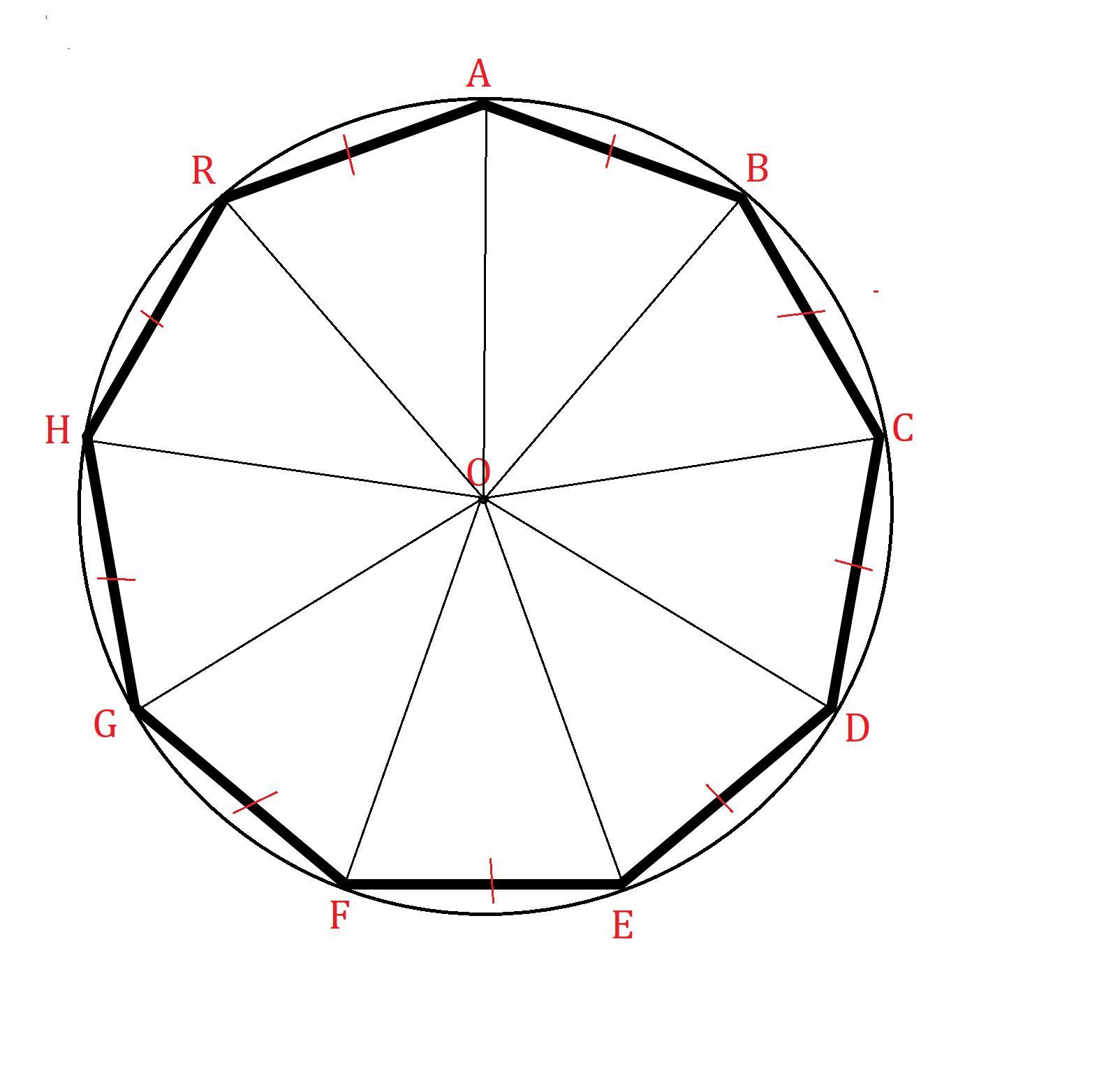
данный многоугольник - девятиугольный.
Обозначим данный девятиугольник буквами .
Около девятиугольника описана окружность с центром в точке
Соединим центр окружности с вершинами данного девятиугольника.
Отрезки - радиусы описанной около девятиугольника окружности, поэтому они равны.
Итак, в данном девятиугольнике 9 равнобедренных равных треугольников:
см (они радиусы описанной окружности).
В окружности всего
Тогда
девятиугольника =
см²
2) 46 см²