Question

Диагональ прямоугольной трапеции разбивает ее на два треугольника, один из которых
является равносторонним со стороной 5. Найдите среднюю линию.

Answer 1

Дано:

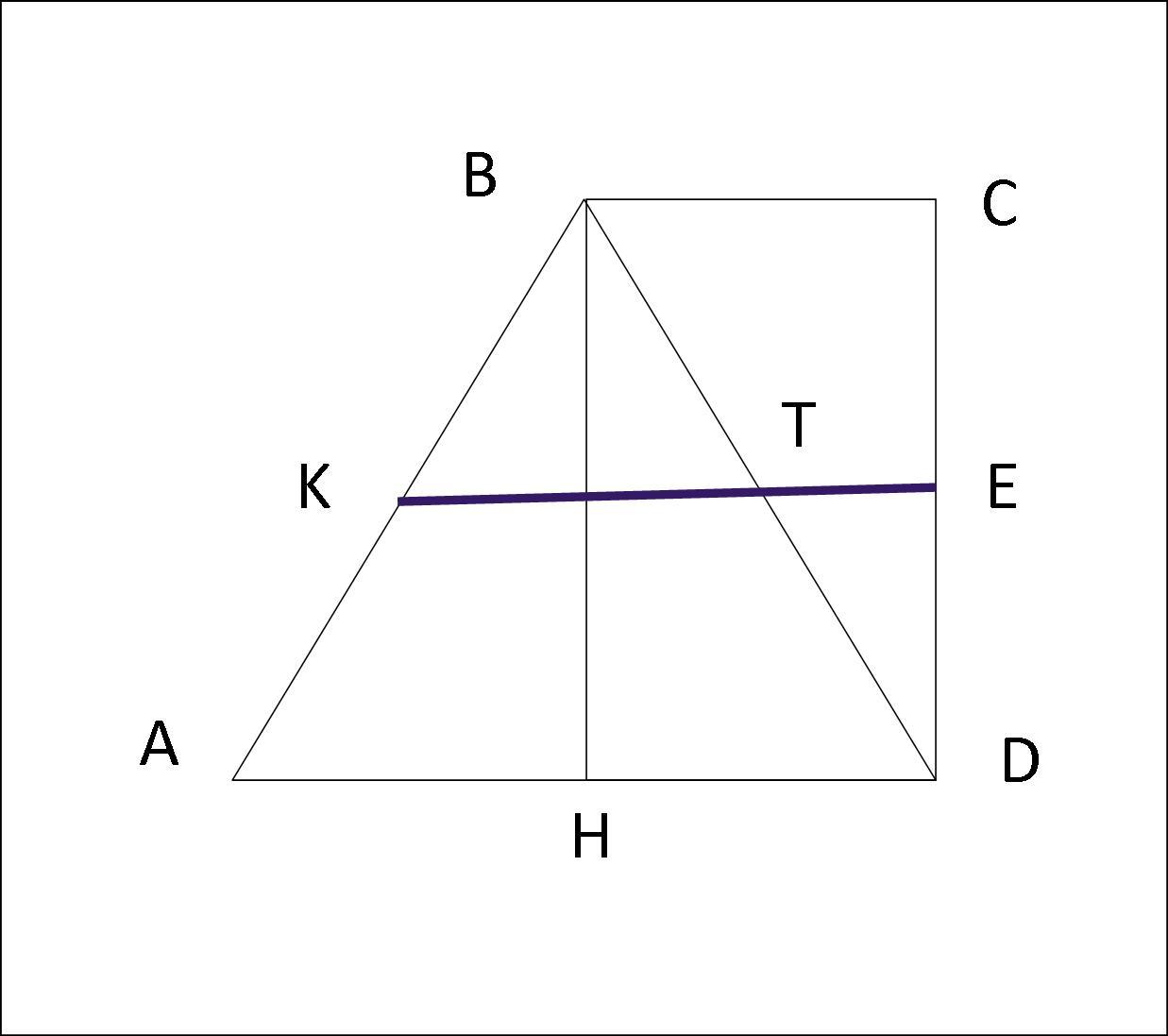
ABCD  - трапеция;

∠ADC=∠BCD=90°

AB=BD=AD=5 см

KE—средняя линия

Найти КЕ

Решение

1) Проведем высоту ВН.

2) Рассмотрим четырёхугольник HBCD.

       ∠BCD=∠CDH =90° по условию;

        ∠BHD=90° по  построению;

Учитывая, что сумма внутренних углов выпуклого четырёхугольника равна 360°, находим четвертый угол:  

∠HBC=360°-(∠BHD +∠BCD+∠CDH)  

∠HBC=360°- 3*90°=90°

Так как у четырёхугольника HBCD все углы прямые, то он является прямоугольником.  

Следовательно, его противоположные стороны равны, т.е.

$BC=HD=\frac{5}{2}=2,5$  см  

3) А теперь находим длину средней линии трапеции ABCD.

$KE = \frac{BC+AD}{2}$

$KE = \frac{2,5+5}{2} =3,75$

$KE = 3,75$ см

Answer 2

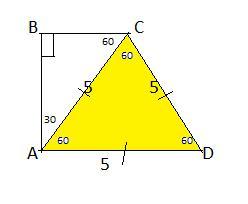
Диагональ прямоугольной трапеции разбивает ее на два треугольника, один из которых  является равносторонним со стороной 5. Найдите среднюю линию.

Пошаговое объяснение:

У равностороннего треугольника все углы по 60°⇒значит он не содержит боковую сторону с прямым углом.

ΔАСD-равносторонний , AD=5 .

АВСD-трапеция ⇒AD║BC , значит ∠CAD=∠BCA как накрест лежащие при секущей ВС.

ΔАВС -прямоугольный, АС-гипотенуза  , ∠ВАС=90°-60°=30°⇒ по свойству угла 30° , ВС=1/2*5=2,5

По свойству средней линии получаем   $\frac{5+2,5}{2} =\frac{5}{2} +\frac{2,5}{2} =2,5+1,25=3,75$