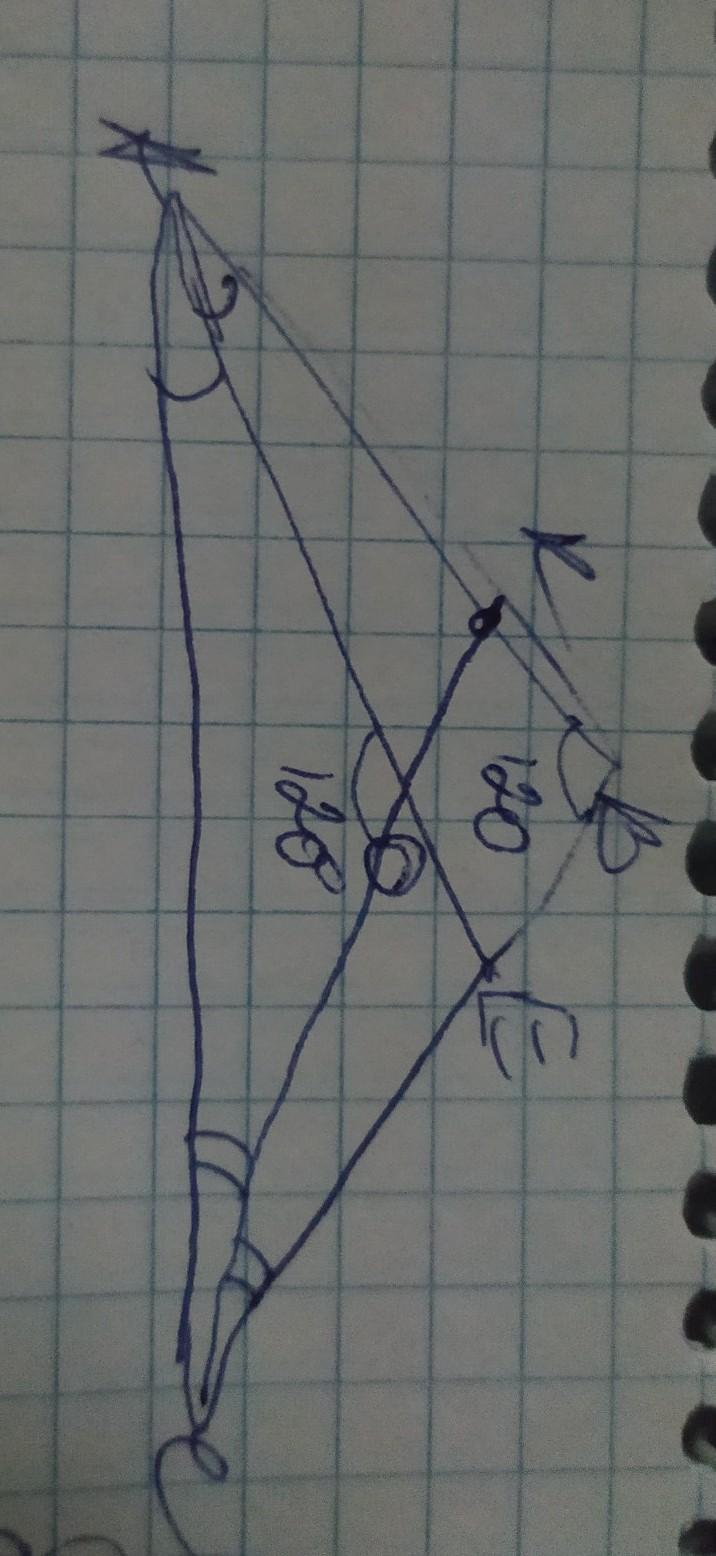
Більший кут трикутника дорівнює 120°. Під яким кутом видно більшу сторону цього трикутника з точки перетину бісектрис гострих кутів трикутника?
Ответы
Ответ:
<АОС=150°
Объяснение:
обозначим вершины треугольника А В С, а его биссектрисы АЕ и СК, а точку их пересечения О. Большую сторону видно под углом АОС, поскольку большая сторона лежит напротив большего угла, поэтому большей стороной будет АС, поскольку она лежит напротив угла В=120° из ∆АВС и
угла АОС из ∆АОС. Мы можем найти угол АОС. Так как биссектриса делит угол пополам, то <ВАЕ=<ЕАС и <ВСК=<АСК. Так как сумма углов треугольника составляет 180°, то в ∆АВС: <А+<С=180–120=60°.
Рассмотрим полученный ∆АОС. Если <А+<С=60°, то <ОАС+<ОСА=60÷2=30°, поскольку эти углы разделены биссектрисами пополам и соответственно сумма этих углов будет в 2 раза меньше суммы углов А и С. Помним, что сумма углов треугольника составляет 180°, поэтому в ∆АОС <В=180–(<ОАС+<ОСА)=180–30=150°