Предмет: Алгебра,
автор: DaniksAST
Если  то
то  будет равно:
будет равно:
Приложения:
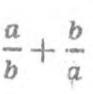
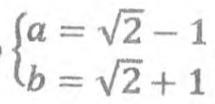
DaniksAST:
Варианты: A) 6 B) 2 C) 8 D) 0 E) 4
Ответы
Автор ответа:
1
Ответ 6
Решение задания прилагаю
Приложения:
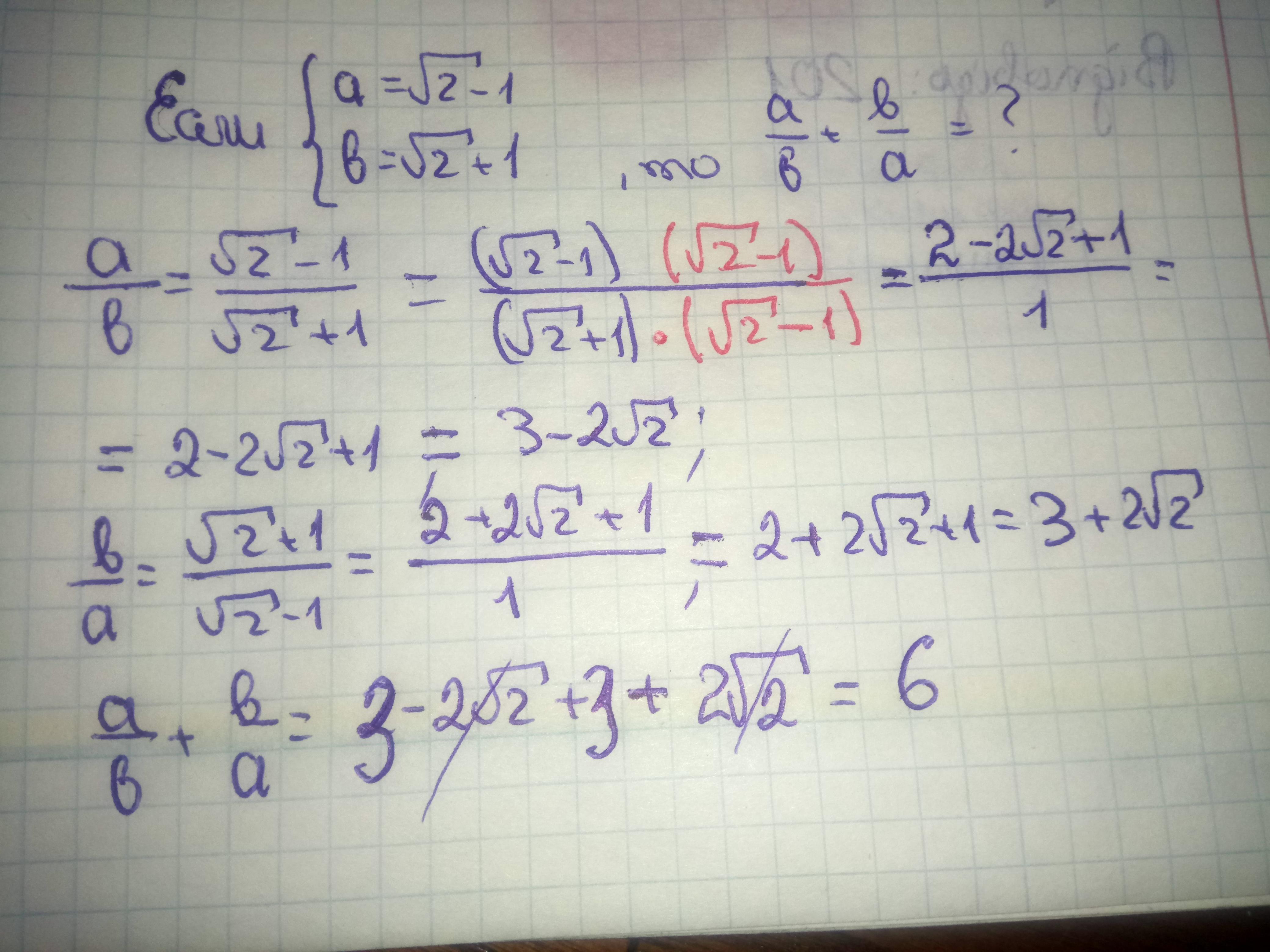

Автор ответа:
1
числитель: (2-2✓2+1) + (2+2√2+1)=6
в знаменатели формула a²-b²=(a-b)(a+b)
знаменатель: 2-1=1
Ответ окончательный =6
Похожие вопросы
Предмет: Русский язык,
автор: лёёёха
Предмет: Русский язык,
автор: polinacat999
Предмет: Другие предметы,
автор: wermik
Предмет: Алгебра,
автор: Begunlol
Предмет: Математика,
автор: ternyavsky2016