Предмет: Математика,
автор: nutaanuta7771
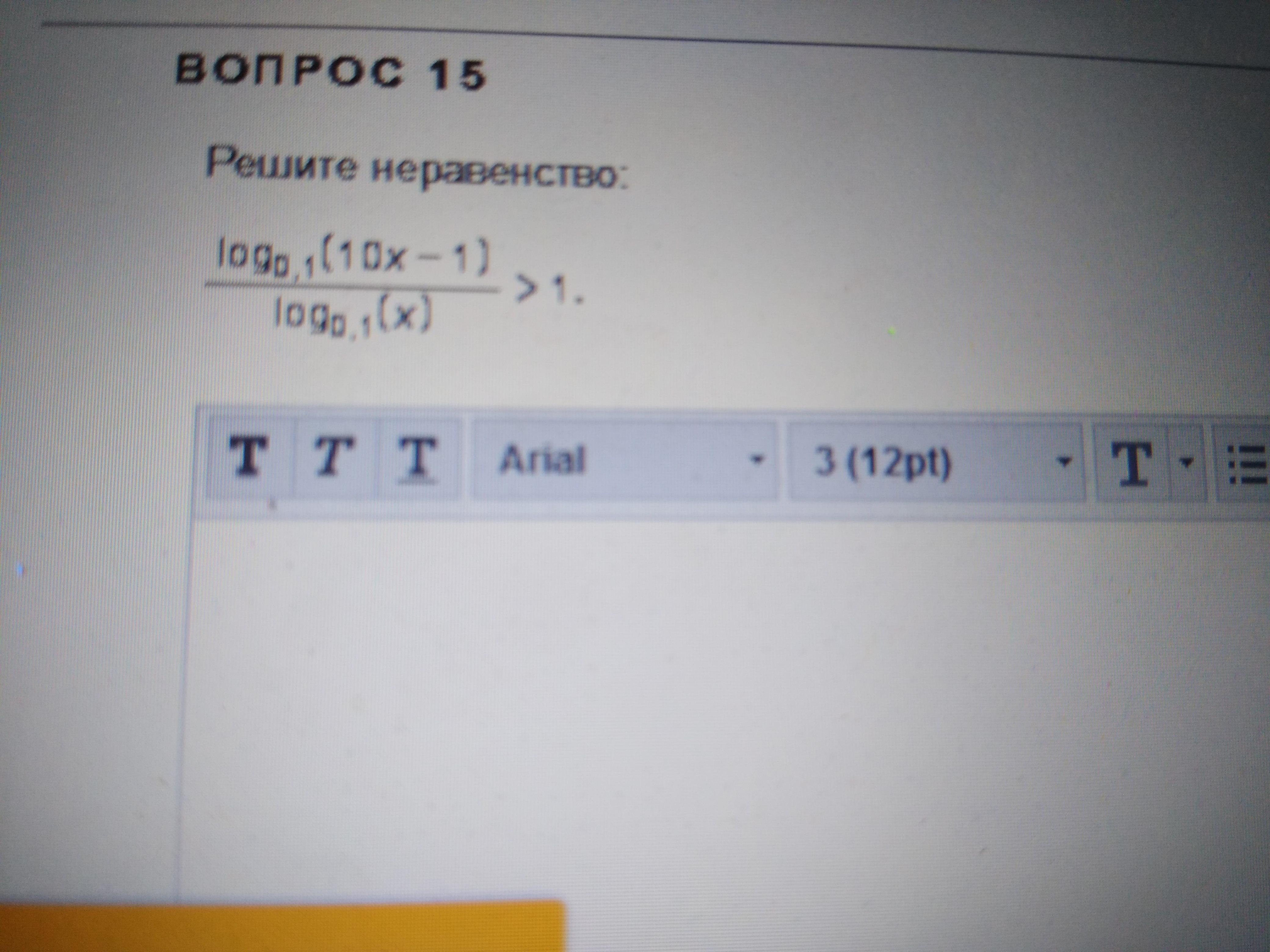
Помогите решить неравенствт пожалуйста!
Приложения:
Ответы
Автор ответа:
0
Ответ:
во вложении...........
Приложения:

Автор ответа:
0
Ответ:
Пошаговое объяснение:
Ограничения:
Решение:
Удобней всего применить метод рационализации:
Корень числителя: 9x-1=0 ⇒ x=1/9
Корень знаменателя: x-1=0 ⇒ x=1
+++(1/9)---(1)+++>x
x∈(-∞;1/9) ∪ (1;+∞)
C учетом ограничений:
x ∈ (0,1; 1/9) ∪ (1;+∞)
Похожие вопросы
Предмет: Другие предметы,
автор: LoveEovlLove
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: likablinova
Предмет: Математика,
автор: anonasssss
Предмет: Математика,
автор: Милкович788