Предмет: Алгебра,
автор: anzhelavinogra83
Помогите, пожалуйста
Приложения:
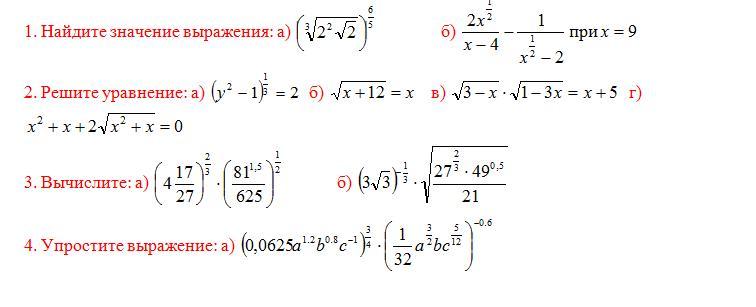
terikovramazan:
многовато
Добавьте баллов. Мб тогда народ появиться)
Ответы
Автор ответа:
0
Ответ:
1.а) 2
б) 0,2
2.а) ±3
б) 4
в) -1
г) 0;1
3. а) 3
б) 1
4.64/c
Объяснение:
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: efanovairina
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Mininikki
Предмет: Химия,
автор: лиса281
Предмет: Математика,
автор: androsova74