Question

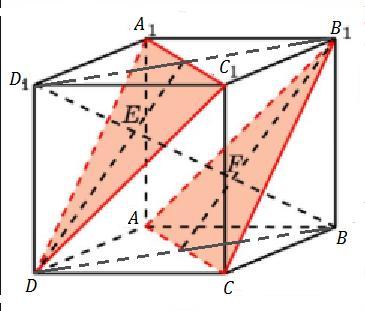
В единичном кубе ABCDA1B1C1D1 найдите расстояние между плоскостями АСВ1 и DC1A1

Answer 1

Ответ:   $d=\dfrac{\sqrt3}{3}\ .$

Диагональ BD1 перпендикулярна параллельным плоскостям  АСВ1  и  DС1А1  и делится в точках пересечения на три равные части .

Следовательно, искомое расстояние равно длине отрезка EF , то есть равно    $EF=\dfrac{1}{3}\cdot BD_1=\dfrac{1}{3}\cdot \sqrt{1^2+1^2+1^2}=\dfrac{\sqrt3}{3}$