Предмет: Геометрия, автор: fiftpmomcvn

Даны точки А, В, С. Найдите точки, равноудаленные от точек А и В, которые находяться на данном расстоянии а от точки С с рисунком

DNHelper: В том и дело, какая разница, где находится точка C? У нас в любом случае будет окружность с радиусом a, которая пересекает/касается/не пересекает серединный перпендикуляр.

DNHelper: https://ibb.co/yS9zxP0 — точки лежат на одной прямой. Что меняется?

Ответы

Автор ответа: DNHelper

Геометрическое место точек, равноудалённых от A и B — серединный перпендикуляр к отрезку AB. Построим окружность с центром C и радиусом a. Тогда точки пересечения данной окружности (если они существуют) с серединным перпендикуляром будут искомыми. Действительно, они лежат одновременно на серединном перпендикуляре, то есть равноудалены от A, B, и на окружности, то есть находятся на расстоянии a (равное радиусу) от C.

Приложения:

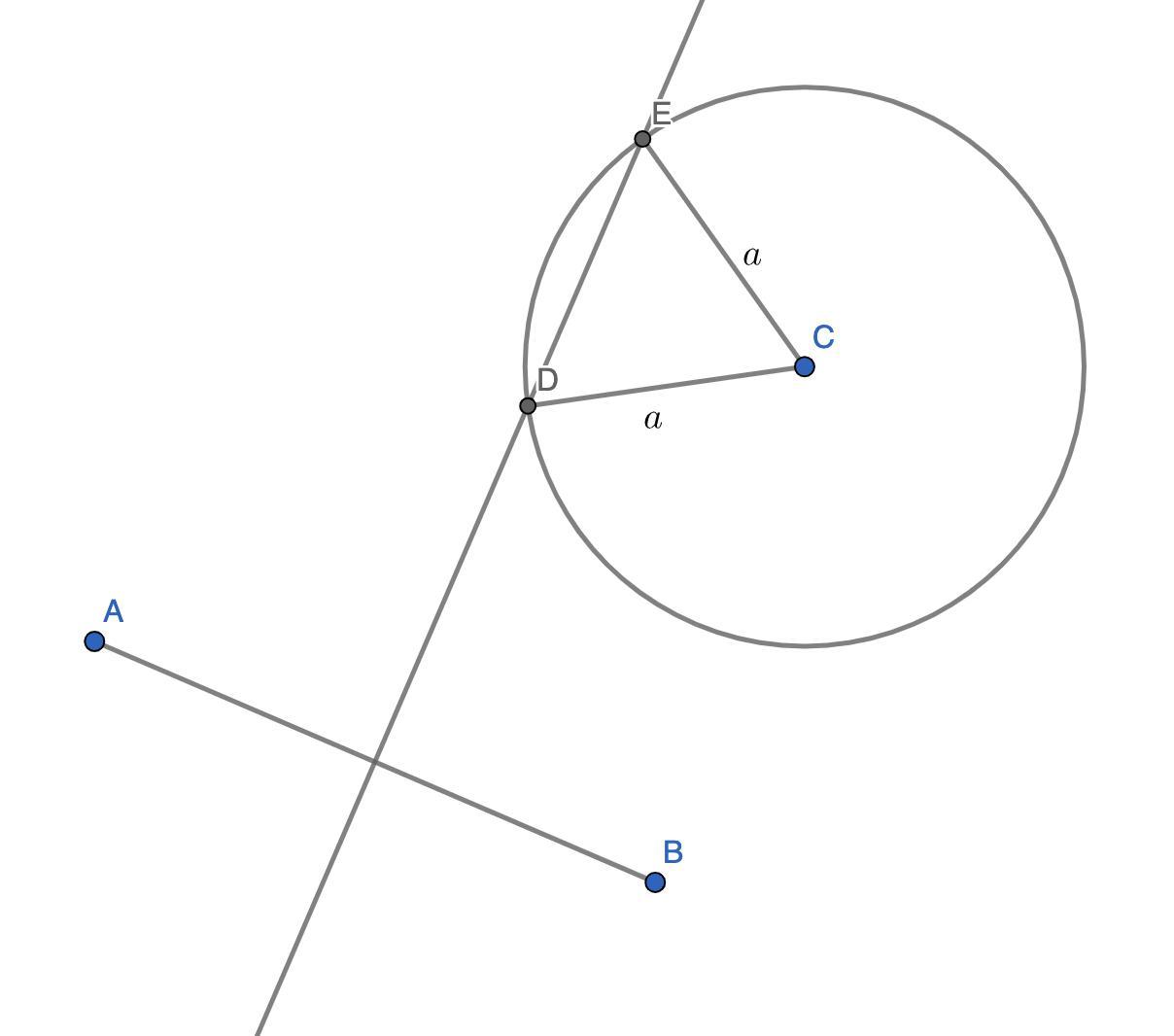
Автор ответа: Аноним

Объяснение:ВО ВЛОЖЕНИИ. ДОБАВЛЮ, что в зависимости от данного расстояния точек может быть две, я это показал, если расстояние равно радиусу окружности, то одна, а если меньше, то ни одной.

Приложения: