Question

•Постройте график функции
y=(7x-5)/(7x2-5x)
Определите при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
• Построите график функции
y=(4|x|-1)/(|x|-4x2)
Определите при каких значениях k прямая y=kx не имеет с графиком общих точек

Answer 1

$y=\frac{7x-5}{7x^2-5x}$

Область определения:

$7x^2-5x\neq 0$

$x(7x-5)\neq 0$

$x\neq 0$  и $x\neq \frac{5}{7}$

Тогда

$y=\frac{7-5}{x(7x-5)}$  

Сократим на  $7x-5$  получим  

$y=\frac{1}{x}$

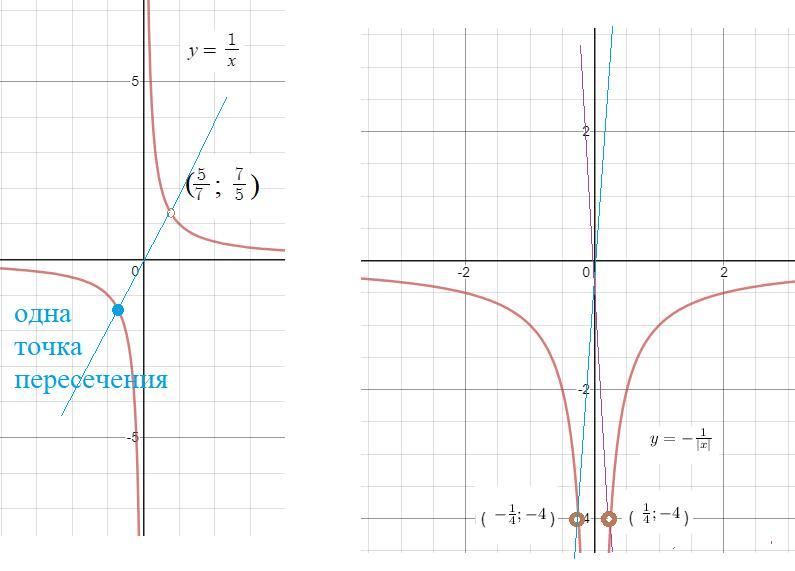
Графики функций     $y=\frac{1}{x}$    и   $y=\frac{7x-5}{7x^2-5x}$

совпадают за исключением  одной точки.

На графике $y=\frac{7x-5}{7x^2-5x}$  нет точки с абсциcсой $x= \frac{5}{7}$

Прямая y=kx, проходящая через точку (  $\frac{5}{7}; \frac{7}{5}$ )  будет иметь с графиком ровно одну общую точку

$\frac{7}{5}=k\cdot \frac{5}{7}$

$k=\frac{49}{25}$

О т в е т. $k=\frac{49}{25}$

2.

$y=\frac{4|x|-1}{|x|-4x^2}$

Область определения:

$|x|-4x^2\neq 0$

$|x|(1-4|x|)\neq 0$

$x\neq 0$  и $x\neq\pm \frac{1}{4}$

Сократим на  $4|x|-1$  получим  

$y=-\frac{1}{|x|}$

Графики функций     $y=-\frac{1}{|x|}$    и   $y=\frac{4|x|-1}{|x|-4x^2}$

совпадают за исключением  двух  точек.

На графике $y=\frac{4|x|-1}{|x|-4x^2}$  нет точек с абсциcсами $x=\pm \frac{1}{4}$

Прямые y=kx, проходящие через точки (  $-\frac{1}{4}; -4$ )    и  (  $\frac{1}{4}; -4$ ) не будут иметь с графиком общих точек

Найдем k:

$4=k\cdot (\pm\frac{1}{4})$

$k=\pm16$

О т в е т. $k=\pm16$