Question

СРОЧНО
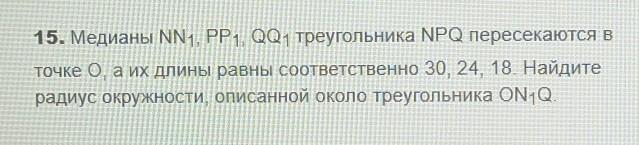
медианы nn1, pp1, qq1 треугольника npq пересекаются в точке о, а их длины​

Answer 1

Найдём сторону PQ, используя формулу:

a = (2/3)*√(2mb² + 2mc² - ma²). Подставим значения.

PQ = (2/3)+√(2*24² + 2*18² - 30²) = (2/3)√900 = 20.

Половина этой стороны равна 20/2 = 10.

Радиус описанной окружности R = abc/(4S).

Так как треугольник равнобедренный, его высота равна √(10² -(12/2)²) = √(100 - 36) = 8.

S = (1/2)*12*8 = 48 кв.ед.

Ответ: R = 10*10*12/(4*48) = 25/4 = 6,25.