Предмет: Алгебра,
автор: selisvet
Решить логарифмическое неравенство
Приложения:
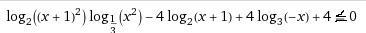
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: aparyna
Предмет: Другие предметы,
автор: naritsakatya
Предмет: Русский язык,
автор: malels
Предмет: Геометрия,
автор: angelochekmari
Предмет: География,
автор: MayMars