Question

С полным решением ,пожалуйста

Answer 1

Решение:

Рассмотрим параллельные прямые прямые AB и CD и их секущую BC. Так как ∠ABC и ∠BCD - внутренние односторонние углы при параллельных прямых , то их сумма равна 180°.

Также, ∠BAD = ∠BCD, по условию. Значит:

∠BAD + ∠ABC = ∠BCD + ∠ABC = 180°.

Получаем, что сумма углов ∠BAD и ∠ABC при прямых AD и BC и секущей AB равна 180°. Значит, AD ║BC.

Связывая это с тем, что AB ║ CD (по условию), получаем, что ABCD - параллелограмм (вспоминаем признак параллелограмма: если у четырехугольника противоположные стороны попарно параллельны, то он является параллелограммом).

Что и требовалось доказать!

Основная идея решения также в четыре формулы отображена в приложении ↓

Answer 2

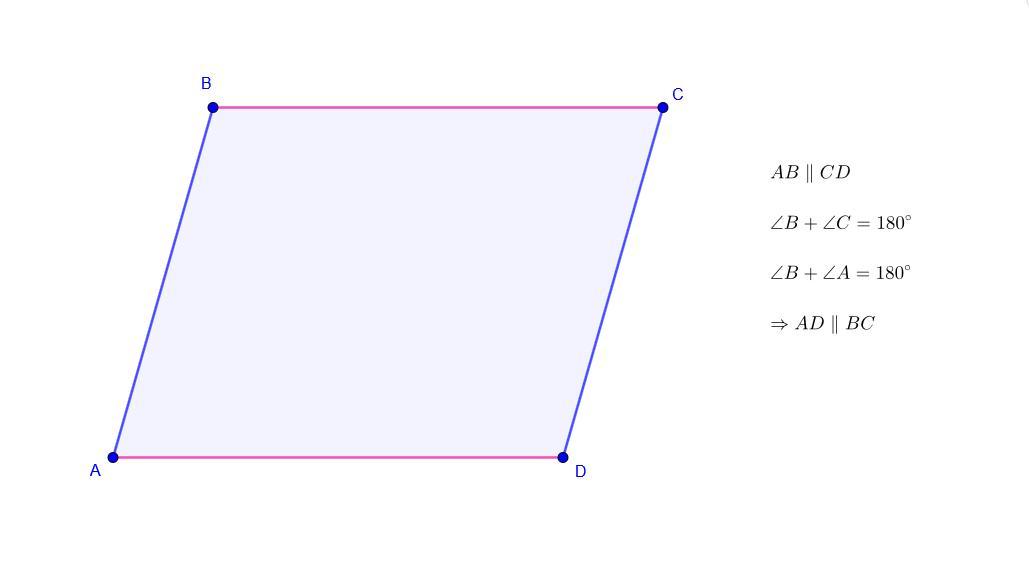
Пошаговое объяснение:

Дано АВСД-четырехугольник,  АВ║СД, ∠А=∠С.

Доказать АВСД -параллелограмм.

Доказательство. Доп. построения -продолжи сторону АД за точку Д. Обозначить угол смежный с углом Д как ∠1.

1)По свойству параллельных прямых с соответственными углами :

∠А=∠1 ,при секущей АД ;

2) По расположению ∠С и ∠1 соответственные и они равны т.к ∠А=∠С⇒ ВС║АД по признаку  параллельности прямых  с накрест лежащими углами.

3) АВСД -параллелограмма по определению параллелограмма : "Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны".