Предмет: Математика,
автор: Jackiea
Помогите с решением пожалуйста
Приложения:
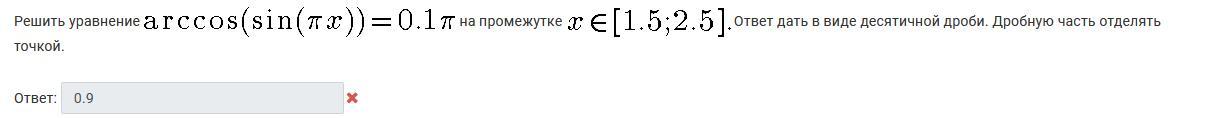
Ответы
Автор ответа:
0
Ответ:
2.4
Пошаговое объяснение:
Для решения понадобится формула приведения:
Также применим: arcsin(sinx)=x, -0.5π≤x≤0.5π; и cos(arccosx)=x; -1≤x≤1
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Английский язык,
автор: aminat2
Предмет: Українська література,
автор: shkirmina25
Предмет: Алгебра,
автор: kisss4
Предмет: Музыка,
автор: nomokonjar