Предмет: Алгебра,
автор: Аноним
30 БАЛЛОВ
ЕГЭ профильная математика,
помогите решить пожалуйста
Приложения:
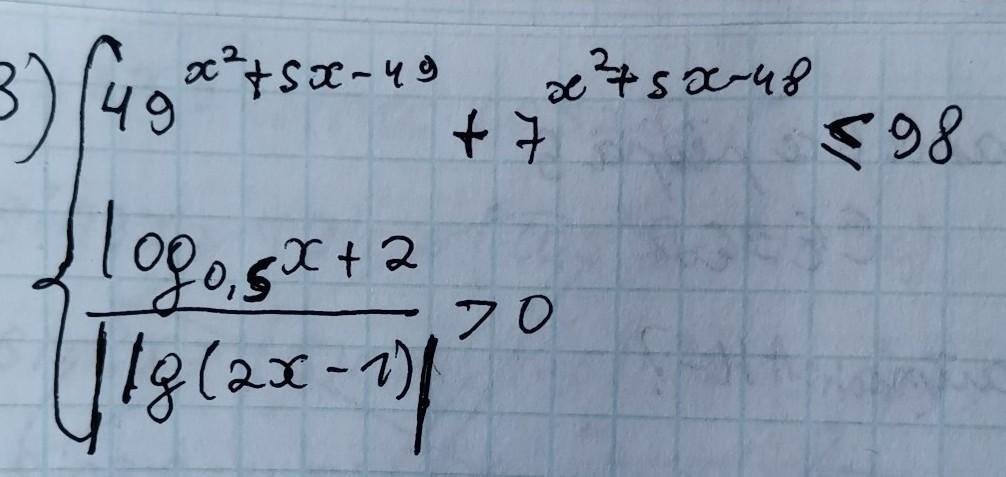
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Решим первое неравенство:
Пусть , тогда неравенство равносильно следующему:
По теореме Виета нули многочлена в левой части t = -98; 49. Тогда
По теореме Виета нули многочлена в левой части x = -10; 5. Тогда
Решим второе неравенство:
ОДЗ:
Заметим, что на ОДЗ знаменатель положителен, так как он стоит под модулем. Значит, чтобы дробь была положительна, числитель тоже должен быть положительным:
C учётом ОДЗ
Пересечём решения:
DNHelper:
Странно, у многих не отображается LaTeX. Попробуйте обновить страницу или посмотрите, как отображается у меня: https://ibb.co/KL8KTxw
Потому что область значений модуля — неотрицательные числа. |3| = 3, |-2| = 2. Нам неважно, что стоит внутри, потому что на выходе мы всегда получаем неотрицательное число (а в данном случае по ОДЗ вообще положительное).
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Українська мова,
автор: liudmylaNabukh
Предмет: Русский язык,
автор: dumitrascu
Предмет: Литература,
автор: kosov240
Предмет: Обществознание,
автор: kristysaf2003