Предмет: Математика,
автор: sproff
Решите уравнение 21
Приложения:
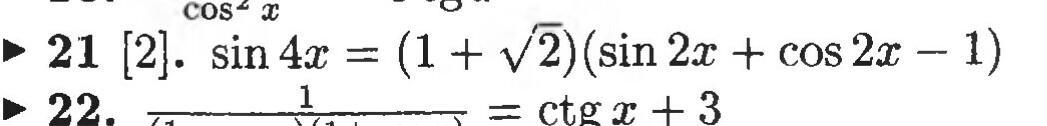
Ответы
Автор ответа:
2
По формуле синуса двойного угла
Уравнение принимает вид:
Замена переменной:
Возводим в квадрат:
⇒
или
Обратная замена:
или
По формулам приведения:
или
По формуле суммы косинусов:
или
или
Так как
или
Так как
или
или
или
О т в е т.
samandararis115:
Спасибо)
Принято))
Спасибо
))
Похожие вопросы
Предмет: Русский язык,
автор: zarinausf
Предмет: Русский язык,
автор: IRA55771
Предмет: Русский язык,
автор: Юлечка155155
Предмет: Алгебра,
автор: 210393
Предмет: Математика,
автор: Zhanyshev83