Предмет: Математика,
автор: vl007panfilov
Решить уравнение при 2 < x < 10
Приложения:
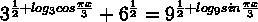
Ответы
Автор ответа:
0
Делим обе части уравнения на
Делим на 2:
Применяем вспомогательный угол:
;
⇒
Применяем формулу косинуса суммы:
⇒
или
Условию 2 < x < 10 удовлетворяют корни:
Похожие вопросы
Предмет: Русский язык,
автор: Zoya3
Предмет: Русский язык,
автор: marinah26
Предмет: Русский язык,
автор: Nastyatalykova
Предмет: Информатика,
автор: asusgaming2k17
Предмет: Математика,
автор: АртоТим