Предмет: Математика,
автор: movielolka
Решите, пожалуйста, пример.
Ответ нужен с решением.
tgx=tg5x
Ответы
Автор ответа:
0
Перенесем все в одну часть:
Представим тангенсы как отношение синуса к косинусу:
Приведем к общему знаменателю:
Заметим в числителе формулу синуса разности:
Дробь равна нулю, когда числитель равен нулю, а знаменателе нулю не равен:
Найдем, при каких х числитель равен нулю:
Найдем при каких х знаменатель обращается в ноль:
Заметим, что вторая серия "посторонних корней" входит в решение
. Значит, их необходимо исключить из решения.
Представив первую серию "посторонних корней" в виде , понимаем, что других посторонних корней в решении
нет.
Таким образом, среди серии корней , обращающих в ноль числитель, встречаются корни
, обращающие в ноль знаменатель. Значит, это посторонние корни, и их необходимо исключить из решения.
Итоговый ответ:
Приложения:
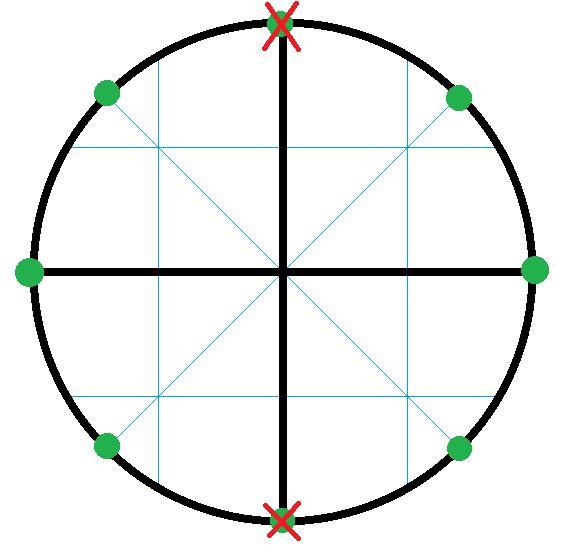
Bublik2223:
..
Похожие вопросы
Предмет: Русский язык,
автор: navolchkova
Предмет: Қазақ тiлi,
автор: nazmustapa
Предмет: Другие предметы,
автор: Мик1
Предмет: История,
автор: HenekoHill
Предмет: Литература,
автор: DASHASNATVORNOE