Question

Прошу помогите пожалуйста.

Answer 1

Ответ:4)

Объяснение:

$\frac{x^{3}(x+1)^{6}(x-2)^{4} ) }{(x-4)(\pi -3)} \leq 0$ - исходное неравенство.

Всё выражение уже разбито на скобки, осталось лишь применить метод интервалов.

Но сначала замечу, что:

1)π > 3- Поэтому скобка (π-3) - положительна и на знак неравенства не влияет.

2) $(x-2)^4$ - находится в чётной степени влияет на знак в точке x = 2, но только если он строгий, но у нас не такой, значит эта скобка не поменяет знак.

3)$(x+1)^6$ - здесь всё так же как и в пункте 2.

4)$(x-4)$ - в точке х = 4 скобка становится равной 0 и тем самым обнуляет знаменатель, а делить на ноль нельзя. Эта скобка имеет нечётную степень, а значит влияет на знак неравенства.

5) $x^{3}$ - имеет нечётную степень влияет на знак.

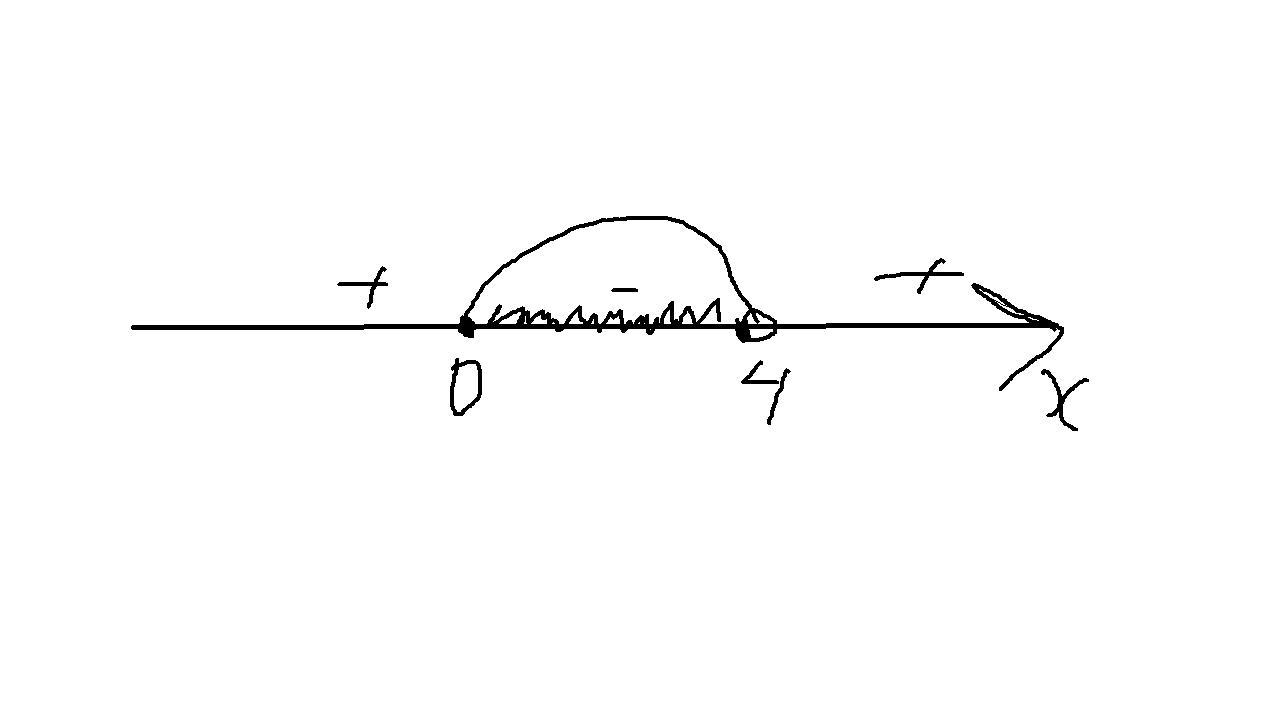
Исходное неравенство можно заменить на равносильное ему :$\left \{ {{x\neq 4} \atop {x(x-4)\leq 0}} \right.$  ; решаем его методом интервалов (см. картинку).

Сложим все целые решения 0+1+2+3 = 6

Ответ: 4)