Question

Найдите все значения параметра а при каждом из которых система уравнений
2х^2+2у^2=4а
4ху=4а-2
имеет всего два решения

Answer 1

Ответ: 0.25

Объяснение:

Разделим оба уравнения на 2:

x^2+y^2 = 2a

2xy =2a-1

вычтем уравнения:

x^2-2xy+y^2 = 1

(x-y)^2 = 1

x-y=+-1

1) y=x+1

2) y=x-1

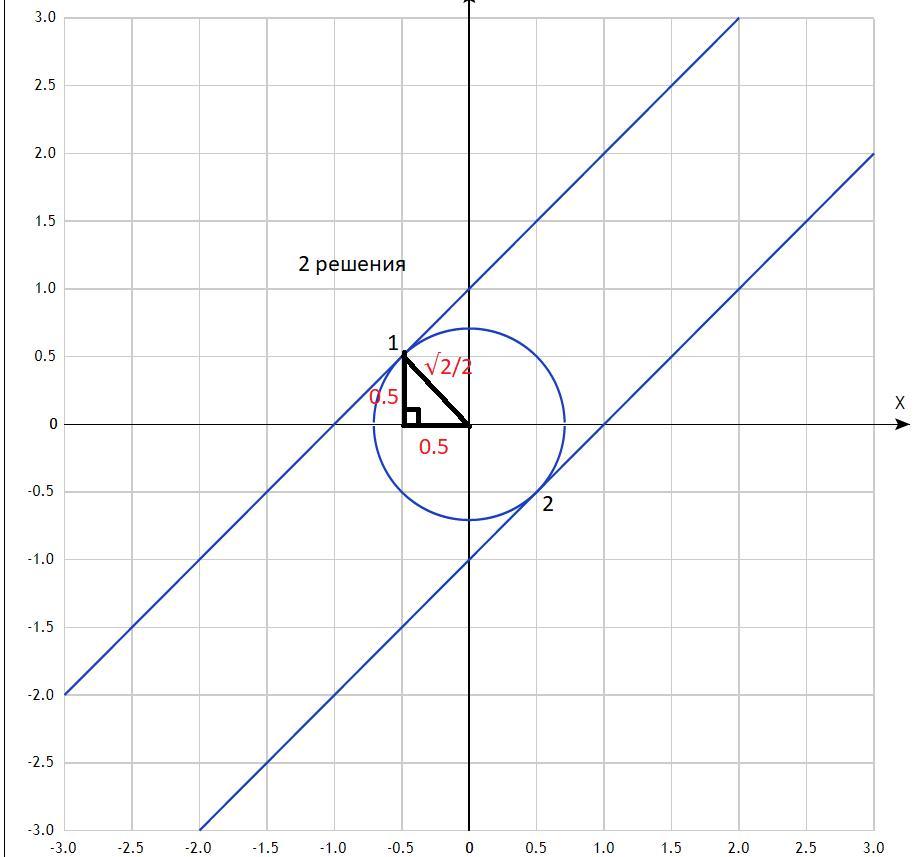
1) ; 2) - две параллельные прямые, которые образуют с началом координат угол 45° , расстояние от начала координат до данных прямых равно √2/2 (по теореме Пифагора)

x^2+y^2 = 2a - окружность с радиусом R=√(2a)  (a>=0)

Если R> √2/2 , то окружность пересекает прямые в 4 точках ( 4 решения).

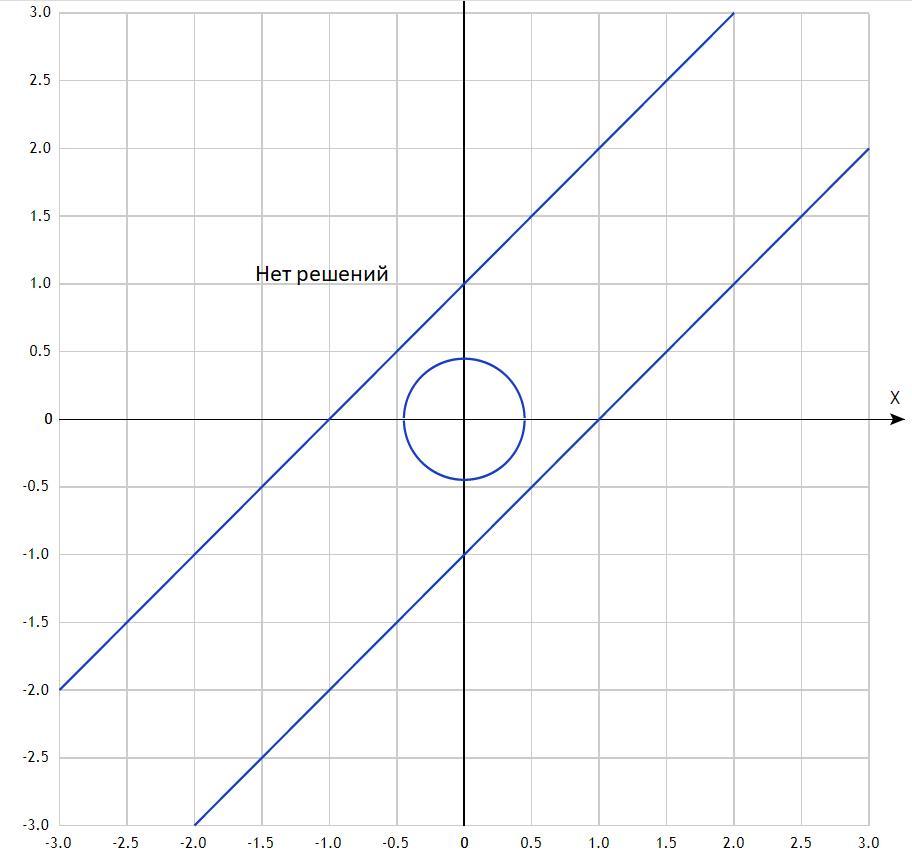
Если R<√2/2, окружность не пересекает прямые (решений нет)

Наконец, если R=√2/2, то окружность касается каждой прямой в одной точке, то есть 2 решения.

√2/2 = √(2a)

a=1/4 = 0.25