Question

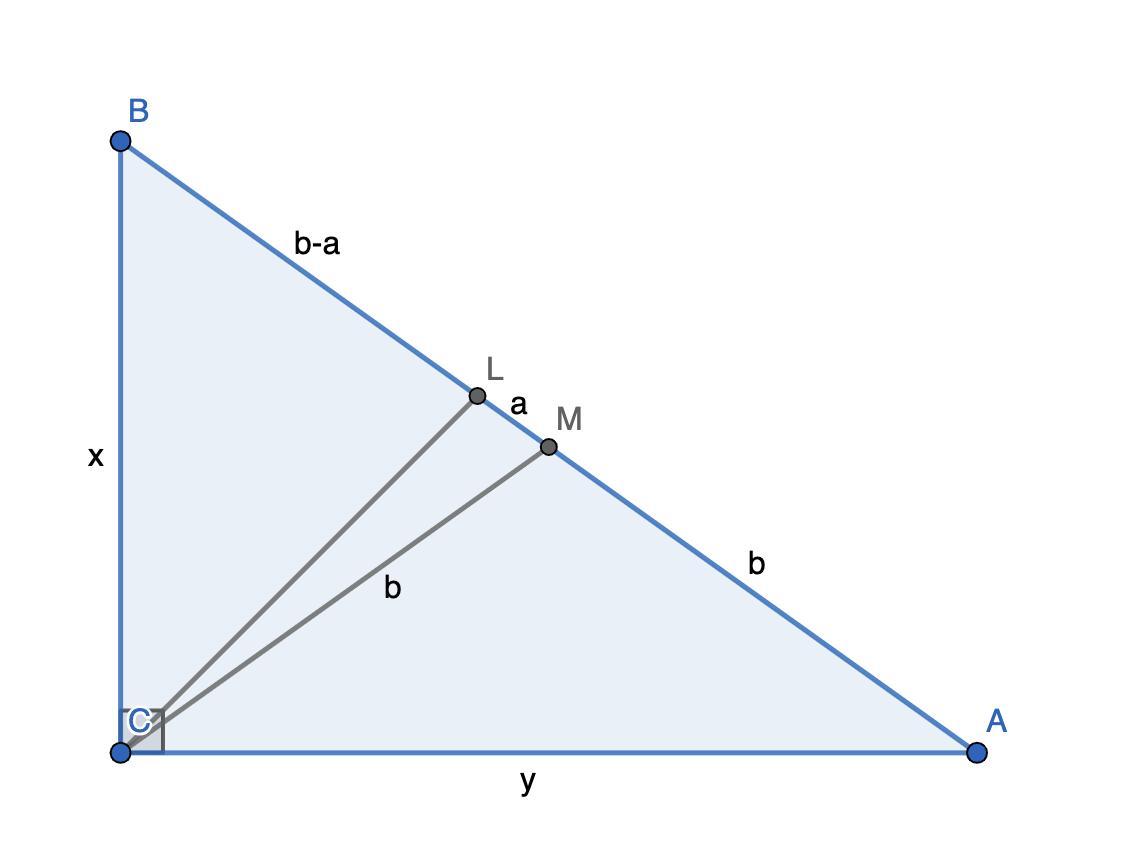
В прямоугольном треугольнике ABC из вершины прямого угла C проведены биссектриса CL и медиана CM. Найдите площадь треугольника ABC, если LM = a, CM = b.

Answer 1

Ответ:

$b^2\cdot\dfrac{b^2-a^2}{b^2+a^2}$

Пошаговое объяснение:

CM — медиана, проведённая из вершины прямого угла ⇒ AM = BM = CM = b. Тогда AL = b + a, BL = b - a (в зависимости от чертежа стороны могут поменяться местами, но суть от этого не поменяется).

Пусть BC = x, AC = y. Тогда по свойству биссектрисы $\dfrac{x}{y}=\dfrac{BL}{AL}=\dfrac{b-a}{b+a}$. Тогда BC = (b - a)k, AC = (b + a)k, k ≠ 0.

По теореме Пифагора:

$(b-a)^2k^2+(b+a)^2k^2=4b^2\\k^2=\dfrac{4b^2}{(b-a)^2+(b+a)^2}=\dfrac{4b^2}{2a^2+2b^2}=\dfrac{2b^2}{a^2+b^2}$

Площадь треугольника $S=\dfrac{1}{2}xy=\dfrac{1}{2}(b-a)(b+a)k^2=\dfrac{b^2-a^2}{2}\cdot\dfrac{2b^2}{a^2+b^2}=b^2\cdot\dfrac{b^2-a^2}{b^2+a^2}$

Answer 2

Ответ:

$\dfrac{b^2(b^2-a^2)}{a^2+b^2}$

Пошаговое объяснение:

Запишем систему:

$\dfrac{AL}{AC}=\dfrac{BL}{BC}\\AC^2+BC^2=AB^2$

Знаем, что медиана в прямоугольном треугольнике, проведенная из вершины прямого угла, равна половине гипотенузы.

Тогда $AB=2b\;=>\;AB^2=4b^2$. Теперь понятно и, что $AL=a+b$ и $BL=b-a$. Учитывая это получим:

$\dfrac{AL^2}{AC^2}=\dfrac{BL^2}{BC^2}\\AC^2=4b^2-BC^2\\\\\dfrac{(a+b)^2}{4b^2-BC^2}=\dfrac{(a-b)^2}{BC^2}\\AC^2=4b^2-BC^2$

Получили уравнение с одной неизвестной BC:

$\dfrac{(a+b)^2}{4b^2-BC^2}=\dfrac{(a-b)^2}{BC^2}$

Выразим BC:

$\dfrac{(a+b)^2}{4b^2-BC^2}=\dfrac{(a-b)^2}{BC^2}\\(a+b)^2BC^2=4b^2(a-b)^2-(a-b)^2BC^2\\(a+b)^2BC^2+(a-b)^2BC^2=4b^2(a-b)^2\\BC^2((a+b)^2+(a-b)^2)=4b^2(a-b)^2\\BC^2(2a^2+2b^2)=4b^2(a-b)^2\\BC^2=\dfrac{4b^2(a-b)^2}{2(a^2+b^2)}\\BC=\dfrac{\sqrt{2}b(b-a)}{\sqrt{a^2+b^2}}$

Теперь выразим AC:

$AC^2=4b^2-BC^2\\AC^2=4b^2-\dfrac{4b^2(a-b)^2}{2(a^2+b^2)}\\AC=\dfrac{\sqrt{2}(ab+b^2)}{\sqrt{a^2+b^2}}$

Теперь найдем площадь:

$S=\dfrac{1}{2}AC\times BC\\S=\dfrac{b(b-a)(ab+b^2)}{a^2+b^2}=\dfrac{b^2(b^2-a^2)}{a^2+b^2}$

Задача решена!