ПОМОГИТЕ ПОЖАЛУЙСТА РАЗОБРАТЬСЯ
СРОЧНО
35 БАЛЛОВ
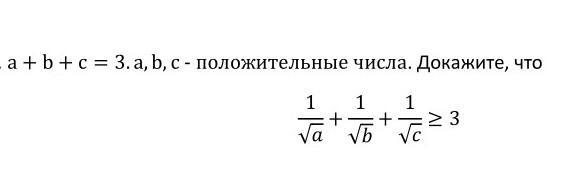
Ответы
Ответ:
По неравенству между средними квадратическим и гармоническим:
Ответ:
Объяснение:
Все переменные в выражении и ограничении равнозначны, нет выделенных. Поэтому условный экстремум, если он есть, будет достигаться при равных значениях переменных a,b и с. Из первого условия следует, что такое значение 1. В точке (1,1,1) функция принимает значение 3. Вычислим значение функции в точке
оно равно
. Значит точка 3 это возможный локальный минимум.
Для поиска условного экстремума запишем функцию Лагранжа и найдем eё экстремум
Приравнивая частные производные к 0, получаем значения для a,b и с.
Как и ожидалось они одинаковые и равны Подставляя в первое условие, получаем
. Точки экстремума 1,1,1
Следующий шаг это определение знака второго дифференциала функции Лагранжа в найденной точке.
Он равен . Значит это точка минимума.