Предмет: Алгебра,
автор: mikooj
ПОМОГИТЕ ПОЖАЛУЙСТА РАЗОБРАТЬСЯ
35 БАЛЛОВ
Приложения:
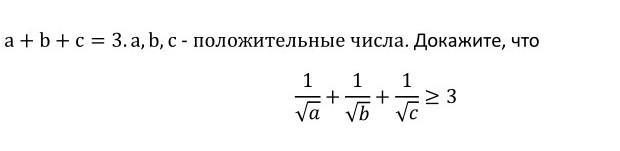
Ответы
Автор ответа:
1
Так как среднее гармоническое меньше или равно среднему геометрическому. а среднее геометрическое меньше или равно среднему арифметическому. среднее арифметическое меньше или равно среднему квадратичному, то по этой цепочке получим, то среднее гармоническое меньше или равно среднему квадратичному трех чисел , значит, можно записать такое неравенство
3/((1/√а)+(1/√b)+(1/√c))≤√(a+b+c)/3, и т.к. а+b+c=3, то
3/((1/√а)+(1/√b)+(1/√c))≤√(3/3); 3/((1/√а)+(1/√b)+(1/√c))≤1, откуда следует
((1/√а)+(1/√b)+(1/√c))≥3. Доказано.
Похожие вопросы
Предмет: Русский язык,
автор: olgajogina2002
Предмет: Русский язык,
автор: ildarkadirov2
Предмет: Русский язык,
автор: kichigina04
Предмет: Обществознание,
автор: anastasia439